Amount of Time for Binary Tree to Be Infected
MediumYou are given the root of a binary tree with unique values, and an integer start. At minute 0, an infection starts from the node with value start.
Each minute, a node becomes infected if:
- The node is currently uninfected.
- The node is adjacent to an infected node.
Return the number of minutes needed for the entire tree to be infected.
Example 1:
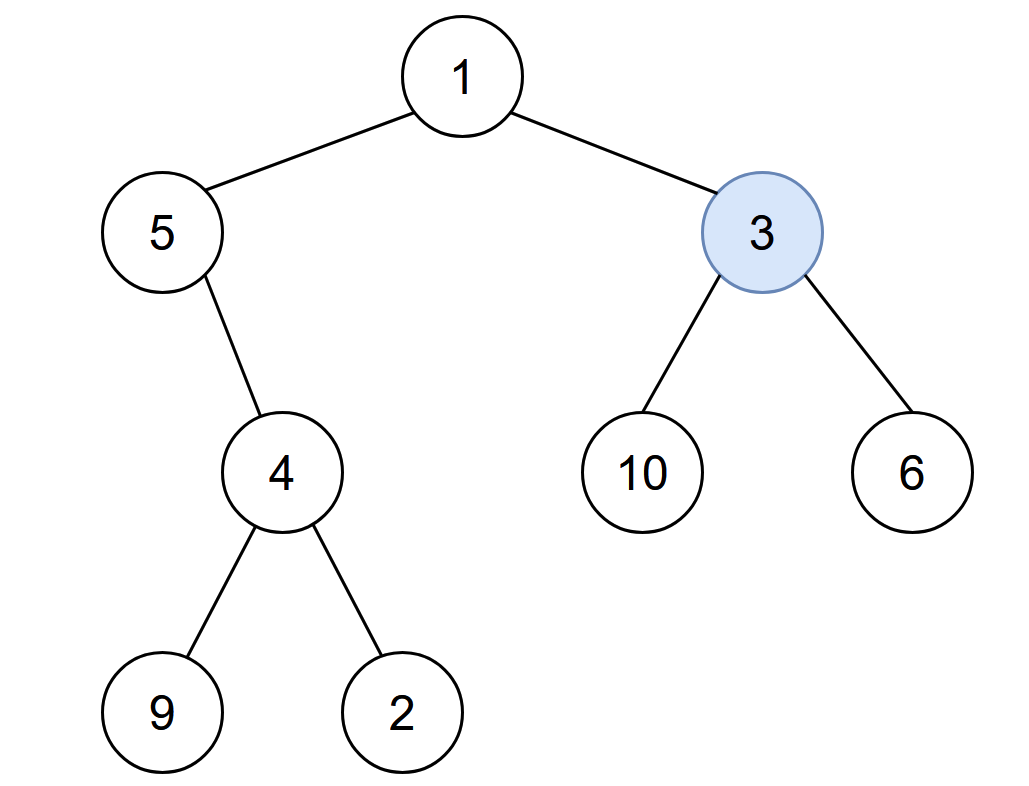
Input: root = [1,5,3,null,4,10,6,9,2], start = 3 Output: 4 Explanation: The following nodes are infected during: - Minute 0: Node 3 - Minute 1: Nodes 1, 10 and 6 - Minute 2: Node 5 - Minute 3: Node 4 - Minute 4: Nodes 9 and 2 It takes 4 minutes for the whole tree to be infected so we return 4.
Example 2:

Input: root = [1], start = 1 Output: 0 Explanation: At minute 0, the only node in the tree is infected so we return 0.
Constraints:
- The number of nodes in the tree is in the range
[1, 105]. 1 <= Node.val <= 105- Each node has a unique value.
- A node with a value of
startexists in the tree.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can the values of nodes in the binary tree be negative, zero, or only positive integers?
- What is the range of values for the nodes in the tree, and how many nodes can the tree contain at most?
- Is the given starting node guaranteed to exist within the binary tree?
- If the tree is empty or the starting node is null, what should I return?
- Do I need to account for the time taken to infect the starting node itself, or does the infection start spreading immediately from it?
Brute Force Solution
Approach
The brute force strategy involves simulating the infection process starting from the initial node. We explore all possible paths and track how long it takes for the entire tree to become infected by trying every possible starting time and spreading from there.
Here's how the algorithm would work step-by-step:
- Imagine starting the infection from the given infected node.
- Now, consider the infection spreading to all the neighbors of the infected nodes at each passing second.
- We want to find the minimum time it takes for the whole tree to become infected.
- So, we can simulate the spread step-by-step, keeping track of which nodes are infected at which second.
- For each node that is not the given infected node we can run the entire infection simulation, starting from the given infected node.
- At the end of the infection simulation we determine how long it took to infect the entire tree.
- Finally, we will have explored all possibilities of infection and determine the minimum time it takes for every node to become infected.
Code Implementation
class TreeNode:
def __init__(self, value=0, left=None, right=None):
self.value = value
self.left = left
self.right = right
def amount_of_time_for_binary_tree_to_be_infected(root, start):
def convert_tree_to_graph(node, graph):
if not node:
return
if node.left:
# Create an edge between the current node and its left child.
graph.setdefault(node.value, []).append(node.left.value)
graph.setdefault(node.left.value, []).append(node.value)
convert_tree_to_graph(node.left, graph)
if node.right:
# Create an edge between the current node and its right child.
graph.setdefault(node.value, []).append(node.right.value)
graph.setdefault(node.right.value, []).append(node.value)
convert_tree_to_graph(node.right, graph)
graph = {}
convert_tree_to_graph(root, graph)
maximum_time = 0
for node_value in graph:
visited = set()
time_elapsed = infect_tree(graph, start, node_value, visited, 0)
maximum_time = max(maximum_time, time_elapsed)
return maximum_time
def infect_tree(graph, start_node, target_node, visited, time):
queue = [(start_node, 0)]
visited.add(start_node)
maximum_time_needed = 0
while queue:
current_node, current_time = queue.pop(0)
if current_node == target_node:
maximum_time_needed = current_time
for neighbor in graph.get(current_node, []):
if neighbor not in visited:
# Track visited nodes to prevent infinite loops
visited.add(neighbor)
queue.append((neighbor, current_time + 1))
all_nodes_infected = True
for node_value in graph:
if node_value not in visited:
all_nodes_infected = False
break
if all_nodes_infected:
return maximum_time_needed
else:
return float('inf')Big(O) Analysis
Optimal Solution
Approach
To figure out how long it takes for a tree to get infected, we'll start at the node that gets infected first. Then, we'll explore the tree outwards from that point, tracking the time it takes for the infection to spread to each node.
Here's how the algorithm would work step-by-step:
- First, find the node in the tree that is initially infected. This is our starting point.
- Imagine the infection spreading like ripples in a pond. We want to explore the tree level by level, starting from the infected node.
- When we go from one node to its parent or to its children, we increase the time it takes for the infection to spread by one unit.
- Keep track of the maximum time it takes for the infection to reach any node in the tree. This will be our final answer.
- To efficiently explore the tree, we'll use a technique that involves storing nodes to visit in the future.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def amount_of_time(root, start):
graph = {}
def build_graph(node):
if not node:
return
if node.left:
if node.val not in graph:
graph[node.val] = []
if node.left.val not in graph:
graph[node.left.val] = []
graph[node.val].append(node.left.val)
graph[node.left.val].append(node.val)
build_graph(node.left)
if node.right:
if node.val not in graph:
graph[node.val] = []
if node.right.val not in graph:
graph[node.right.val] = []
graph[node.val].append(node.right.val)
graph[node.right.val].append(node.val)
build_graph(node.right)
build_graph(root)
# BFS is used to explore the graph from the start node.
queue = [(start, 0)]
visited = {start}
max_time = 0
while queue:
node, time = queue.pop(0)
max_time = max(max_time, time)
# Check neighbors to avoid cycles and to explore new nodes.
if node in graph:
for neighbor in graph[node]:
if neighbor not in visited:
queue.append((neighbor, time + 1))
visited.add(neighbor)
# The maximum time represents the time to infect all nodes.
return max_timeBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null root node | Return 0 if the root is null, as there's no tree to infect. |
| Single node tree where that node is the start node | Return 0, as the infection starts and completes instantly at that node. |
| Start node not found in the tree | Return -1 or throw an exception to indicate start node is not present. |
| Tree is a linear chain (skewed left or right) | The traversal and infection time will be proportional to the chain's length, which tests the algorithm's performance on extreme cases. |
| Tree is a complete binary tree with a very large number of nodes | Ensure the solution avoids excessive recursion depth, potentially using iterative methods or optimizing recursion, as a stack overflow could occur. |
| Start node is the root node | The algorithm should correctly calculate the maximum distance to any leaf or node in the tree from the root. |
| All nodes have the same value (including the start node) | This won't impact the algorithm functionally as the infection spreads based on node connections, not values. |
| Tree with duplicate node values but a unique start node value | The algorithm needs to correctly identify the specific start node, and infection spreads from that particular node. |