Binary Search Tree Iterator

Medium

Asked by:

65 views

Topics:

TreesStacks

Implement the BSTIterator class that represents an iterator over the in-order traversal of a binary search tree (BST):

BSTIterator(TreeNode root) Initializes an object of the BSTIterator class. The root of the BST is given as part of the constructor. The pointer should be initialized to a non-existent number smaller than any element in the BST.
boolean hasNext() Returns true if there exists a number in the traversal to the right of the pointer, otherwise returns false.
int next() Moves the pointer to the right, then returns the number at the pointer.

Notice that by initializing the pointer to a non-existent smallest number, the first call to next() will return the smallest element in the BST.

You may assume that next() calls will always be valid. That is, there will be at least a next number in the in-order traversal when next() is called.

Example 1:

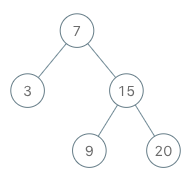
Input
["BSTIterator", "next", "next", "hasNext", "next", "hasNext", "next", "hasNext", "next", "hasNext"]
[[[7, 3, 15, null, null, 9, 20]], [], [], [], [], [], [], [], [], []]
Output
[null, 3, 7, true, 9, true, 15, true, 20, false]

Explanation
BSTIterator bSTIterator = new BSTIterator([7, 3, 15, null, null, 9, 20]);
bSTIterator.next();    // return 3
bSTIterator.next();    // return 7
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 9
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 15
bSTIterator.hasNext(); // return True
bSTIterator.next();    // return 20
bSTIterator.hasNext(); // return False

Constraints:

The number of nodes in the tree is in the range [1, 10⁵].
0 <= Node.val <= 10⁶
At most 10⁵ calls will be made to hasNext, and next.

Follow up:

Could you implement next() and hasNext() to run in average O(1) time and use O(h) memory, where h is the height of the tree?

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

Can the BST be empty, and if so, what should `hasNext()` return initially and what should `next()` do?
What is the range of values that the nodes in the BST can hold? Are they integers, or can they be other data types?
Are duplicate values allowed in the BST, and if so, how should they be handled during in-order traversal?
Is it acceptable to modify the original BST during the initialization or iteration process?
What are the memory constraints? Is it acceptable to store the entire in-order traversal in memory, or should I use a more space-efficient approach?

Brute Force Solution

Approach

The brute force approach for iterating through a Binary Search Tree (BST) involves getting all the values first. We essentially extract all the node values from the tree into a list upfront, then use that list to simulate the iterator's behavior.

Here's how the algorithm would work step-by-step:

First, we walk through the entire BST and collect all the node values.
We store these node values in a simple list, making sure to arrange them in increasing order as we go (smallest to largest). This is important for the iterator to work correctly.
To 'move to the next smallest' value, we just grab the next number from our list, as the list is already sorted.
To check if there is 'another value available', we simply see if we have reached the end of the list or not.

Code Implementation

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class BSTIterator:

    def __init__(self, root: TreeNode):
        self.sorted_values = []
        self.current_index = 0
        self.inorder_traversal(root)

    def inorder_traversal(self, root: TreeNode):
        if root:
            self.inorder_traversal(root.left)
            self.sorted_values.append(root.val)
            self.inorder_traversal(root.right)

    def next(self) -> int:
        # Return the next smallest element
        next_smallest_element = self.sorted_values[self.current_index]
        self.current_index += 1
        return next_smallest_element

    def hasNext(self) -> bool:
        # Check if there is another element
        return self.current_index < len(self.sorted_values)

Big(O) Analysis

Time Complexity

O(n) – The time complexity is determined by two main operations: traversing the BST to collect all node values and then iterating through the stored values. Traversing the BST visits each node exactly once, resulting in O(n) time complexity, where n is the number of nodes in the tree. The subsequent operations to get the next smallest value and check if there is another value take O(1) time since they simply access elements from a pre-computed and sorted list. Therefore, the overall time complexity is dominated by the initial BST traversal, giving a total time complexity of O(n).

Space Complexity

O(N) – The brute force solution first traverses the entire Binary Search Tree and stores all N node values in a list, where N is the total number of nodes in the BST. This list is used to simulate the iterator. Therefore, the auxiliary space required to store the sorted list of node values grows linearly with the number of nodes in the tree. This results in a space complexity of O(N).

Optimal Solution

Approach

The best way to go through a binary search tree 'in order' (smallest to largest) without extra memory is to use a stack to keep track of our progress. We'll essentially simulate the recursive inorder traversal iteratively, keeping track of the path we've taken.

Here's how the algorithm would work step-by-step:

Start at the root of the tree.
Go as far left as possible from the current node, adding each node we visit to a stack. Think of the stack as a breadcrumb trail of where we've been.
When we hit a dead end (a node with no left child), pop the last node from the stack. This is the next smallest value.
If that node has a right child, start the process over again from the right child.
If that node does not have a right child, simply return to the stack until we are back to root.
Keep repeating steps until the stack is empty, meaning we've processed every node in the tree.

Code Implementation

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right

class BSTIterator:

    def __init__(self, root: TreeNode):
        self.stack_of_nodes = []
        self._push_left(root)

    def _push_left(self, node: TreeNode):
        # Traverse left, adding nodes to stack
        while node:
            self.stack_of_nodes.append(node)
            node = node.left

    def next(self) -> int:
        # Pop the smallest, prepare for the next
        current_node = self.stack_of_nodes.pop()

        # If there's a right, push its left children
        if current_node.right:
            self._push_left(current_node.right)

        return current_node.val

    def hasNext(self) -> bool:
        # True if there's still nodes in stack
        return len(self.stack_of_nodes) > 0

# Your BSTIterator object will be instantiated and called as such:
# bSTIterator = BSTIterator(root)
# while bSTIterator.hasNext():
#     print(bSTIterator.next())

Big(O) Analysis

Time Complexity

O(n) – The hasNext() operation has an amortized time complexity of O(1), and the next() operation also has an amortized time complexity of O(1). This is because each node is pushed onto the stack and popped from the stack only once. Since we visit each of the n nodes in the binary search tree exactly once during the entire in-order traversal, the overall time complexity for iterating through all nodes is O(n). Therefore the Big O for the entire iterator is O(n).

Space Complexity

O(H) – The algorithm utilizes a stack to store nodes encountered while traversing as far left as possible from the current node. In the worst-case scenario, the stack will contain all the nodes along the longest path from the root to a leaf. This path corresponds to the height (H) of the tree, where N is the total number of nodes in the tree. Therefore, the auxiliary space required for the stack is proportional to the height of the tree, and the space complexity is O(H). In a balanced tree, H is log(N), but in a skewed tree, H can be N.

Edge Cases

Case	How to Handle
Root is null	The constructor should initialize an empty stack, and hasNext() should return false.
BST with only a root node	hasNext() should return true initially, next() should return the root's value once, and then hasNext() should return false.
Skewed BST (left-leaning or right-leaning)	The algorithm's space complexity will depend on the height of the tree, so a skewed tree will result in O(N) space usage (where N is the number of nodes).
BST with duplicate values	The in-order traversal will still correctly return the nodes in sorted order, including duplicates.
Large BST (many nodes)	The iterative in-order traversal using a stack should be efficient enough, and its space consumption depends on the height of the tree, which will be O(log N) for a balanced BST and O(N) for a skewed BST.
BST containing negative and/or zero values	The algorithm works correctly with negative and zero values since it only relies on the BST property (left < node < right).
Extremely large or small integer values in nodes	Ensure the language's integer type can handle the node values without overflow or underflow during comparisons.
Calling next() after hasNext() returns false	Define the behavior, such as throwing an exception or returning null, when calling next() on an exhausted iterator.

Root is null

How to Handle:

The constructor should initialize an empty stack, and hasNext() should return false.

BST with only a root node

How to Handle:

hasNext() should return true initially, next() should return the root's value once, and then hasNext() should return false.

Skewed BST (left-leaning or right-leaning)

How to Handle:

The algorithm's space complexity will depend on the height of the tree, so a skewed tree will result in O(N) space usage (where N is the number of nodes).

BST with duplicate values

How to Handle:

The in-order traversal will still correctly return the nodes in sorted order, including duplicates.

Large BST (many nodes)

How to Handle:

The iterative in-order traversal using a stack should be efficient enough, and its space consumption depends on the height of the tree, which will be O(log N) for a balanced BST and O(N) for a skewed BST.

BST containing negative and/or zero values

How to Handle:

The algorithm works correctly with negative and zero values since it only relies on the BST property (left < node < right).

Extremely large or small integer values in nodes

How to Handle:

Ensure the language's integer type can handle the node values without overflow or underflow during comparisons.

Calling next() after hasNext() returns false

How to Handle:

Define the behavior, such as throwing an exception or returning null, when calling next() on an exhausted iterator.