Binary Tree Pruning
MediumGiven the root of a binary tree, return the same tree where every subtree (of the given tree) not containing a 1 has been removed.
A subtree of a node node is node plus every node that is a descendant of node.
Example 1:

Input: root = [1,null,0,0,1] Output: [1,null,0,null,1] Explanation: Only the red nodes satisfy the property "every subtree not containing a 1". The diagram on the right represents the answer.
Example 2:
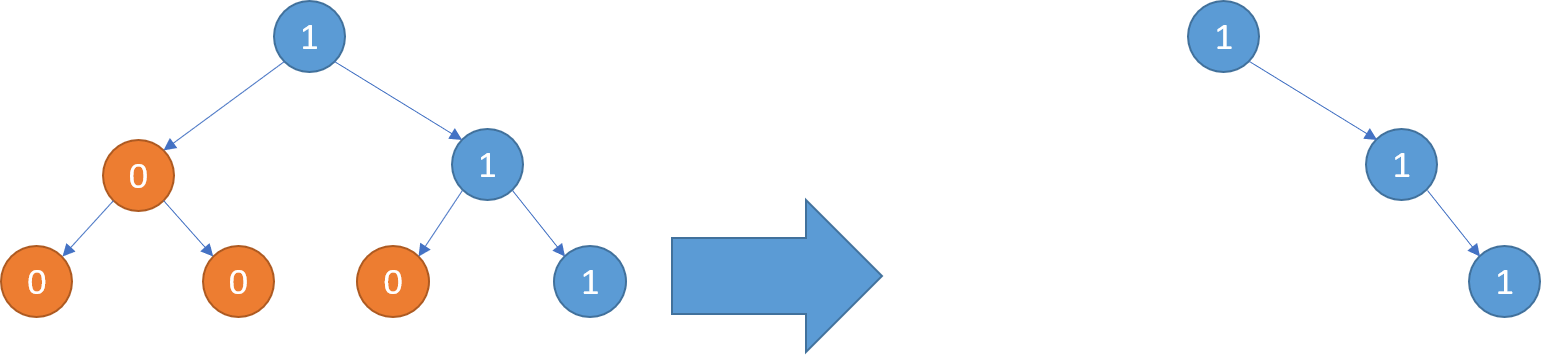
Input: root = [1,0,1,0,0,0,1] Output: [1,null,1,null,1]
Example 3:
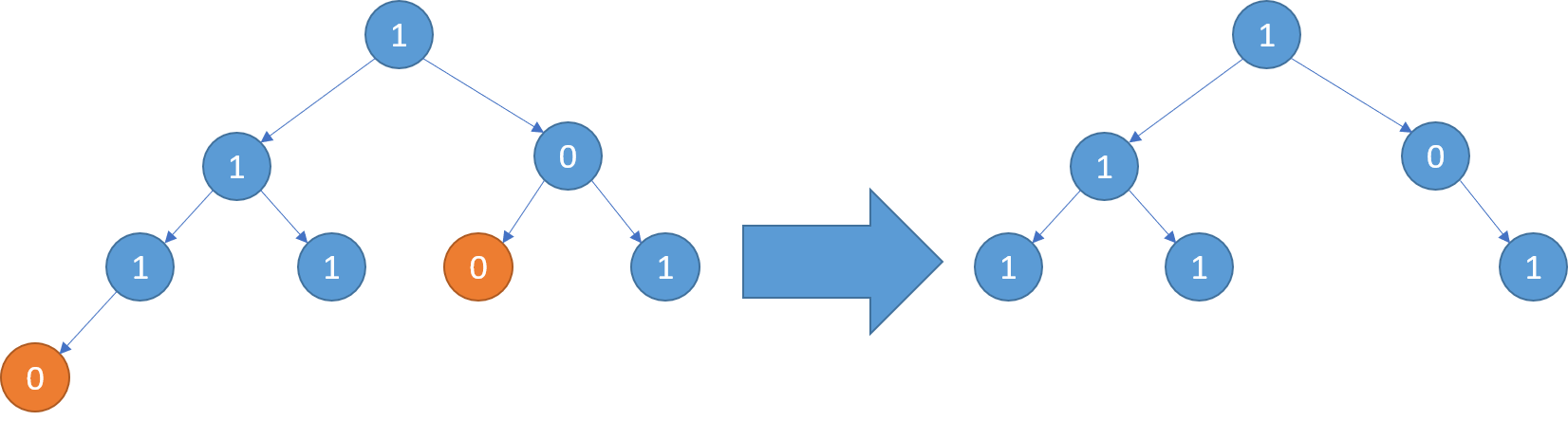
Input: root = [1,1,0,1,1,0,1,0] Output: [1,1,0,1,1,null,1]
Constraints:
- The number of nodes in the tree is in the range
[1, 200]. Node.valis either0or1.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for the nodes in the binary tree? Are negative values possible?
- What should I return if the root is null or if the tree becomes entirely empty after pruning?
- If a node has value '0' but one of its subtrees needs to be kept, should that node be kept as well?
- Can I modify the original tree structure directly, or should I create and return a new pruned tree?
- Are the node values integers, or could they be floating-point numbers?
Brute Force Solution
Approach
The goal is to remove parts of a tree that are all zeros. A brute force approach checks every single part of the tree to see if it can be removed. It explores all possible combinations of removing or keeping each part.
Here's how the algorithm would work step-by-step:
- Start by looking at the very top of the tree.
- Decide whether to keep it or remove it.
- If you keep it, look at the next level down on the left side, and decide whether to keep that or remove it.
- Do the same thing for the right side of the top.
- Keep going down the tree, level by level, making a choice at each part whether to keep it or remove it.
- After you've reached the bottom and made all your keep/remove choices, check if the whole tree is now just zeros.
- If it is, this is a possible solution.
- Do this over and over again, trying EVERY possible combination of keeping and removing parts.
- Once you've tried every single combination, choose the one that removes as many unnecessary zeros as possible while still following the rules.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def pruneTreeBruteForce(root):
def is_all_zeros(node):
if not node:
return True
if node.val != 0:
return False
return is_all_zeros(node.left) and is_all_zeros(node.right)
def all_possible_trees(node):
if not node:
return [None]
left_trees = all_possible_trees(node.left)
right_trees = all_possible_trees(node.right)
possible_trees = []
for left_tree in left_trees:
for right_tree in right_trees:
# Keep current node, explore its children.
new_node = TreeNode(node.val, left_tree, right_tree)
possible_trees.append(new_node)
# Prune left.
new_node = TreeNode(node.val, None, right_tree)
possible_trees.append(new_node)
# Prune right.
new_node = TreeNode(node.val, left_tree, None)
possible_trees.append(new_node)
# Prune both children.
new_node = TreeNode(node.val, None, None)
possible_trees.append(new_node)
return possible_trees
possible_trees = all_possible_trees(root)
best_tree = None
max_nodes_removed = -1
for possible_tree in possible_trees:
if possible_tree is None:
if max_nodes_removed < 0:
max_nodes_removed = 0
best_tree = None
continue
if is_all_zeros(possible_tree):
nodes_removed = count_nodes(root) if root else 0
else:
nodes_removed = count_nodes(root) - count_nodes(possible_tree)
if nodes_removed > max_nodes_removed:
# Found a better pruned tree.
max_nodes_removed = nodes_removed
best_tree = possible_tree
return best_tree
def count_nodes(root):
if not root:
return 0
return 1 + count_nodes(root.left) + count_nodes(root.right)Big(O) Analysis
Optimal Solution
Approach
The goal is to remove parts of a tree that are not important. We'll go through the tree from the bottom up, deciding at each point whether to keep it or cut it off based on what's below.
Here's how the algorithm would work step-by-step:
- Start at the very bottom of the tree, at the leaves.
- Look at each leaf: If it's a zero, we can get rid of it.
- Move up to the nodes just above the leaves. For each node, check its children. If both children are gone (because they were zero or already cut off), and the node itself is a zero, then get rid of the node too.
- Keep going up the tree, level by level. At each node, check if its children are gone and if the node itself is zero. If so, remove it.
- Repeat this process until you reach the very top of the tree. The remaining tree is the pruned version.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def pruneTree(root):
# type root: TreeNode
# type: -> TreeNode
def prune_subtree(node):
if not node:
return None
node.left = prune_subtree(node.left)
node.right = prune_subtree(node.right)
# If node is zero and has no children, prune it.
if node.val == 0 and not node.left and not node.right:
return None
# We need to keep the node in other cases.
return node
# Kick off the recursive pruning process
return prune_subtree(root)Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or Empty Tree | Return null immediately as there is nothing to prune. |
| Tree with a single node (root) | Check the root node's val; if it's 0, return null; otherwise, return the root. |
| Tree with all nodes having value 0 | The pruning should result in a null tree and the algorithm should correctly prune all nodes. |
| Tree with all nodes having value 1 | The tree remains unchanged after pruning as no node is pruned. |
| Skewed tree (e.g., all nodes on the left) | The recursive calls should handle the skewed nature without stack overflow (within reasonable tree depth limits), correctly pruning 0-valued branches. |
| Deeply nested tree leading to stack overflow (language dependent) | Consider an iterative approach or tail-call optimization (if the language supports it) to prevent stack overflow for extremely deep trees. |
| Tree with a large number of nodes (memory constraints) | Ensure the pruning algorithm is efficient in terms of memory usage to avoid out-of-memory errors. |
| Subtree with a non-zero value near a zero-valued root | The recursive post-order traversal ensures that the subtree is visited before the root, preserving it. |