Bulb Switcher
MediumThere are n bulbs that are initially off. You first turn on all the bulbs, then you turn off every second bulb.
On the third round, you toggle every third bulb (turning on if it's off or turning off if it's on). For the ith round, you toggle every i bulb. For the nth round, you only toggle the last bulb.
Return the number of bulbs that are on after n rounds.
Example 1:
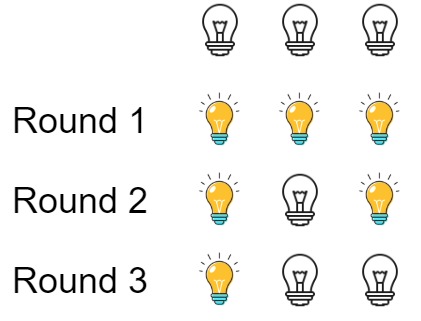
Input: n = 3 Output: 1 Explanation: At first, the three bulbs are [off, off, off]. After the first round, the three bulbs are [on, on, on]. After the second round, the three bulbs are [on, off, on]. After the third round, the three bulbs are [on, off, off]. So you should return 1 because there is only one bulb is on.
Example 2:
Input: n = 0 Output: 0
Example 3:
Input: n = 1 Output: 1
Constraints:
0 <= n <= 109
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the maximum number of bulbs (n) we should expect, and are there any constraints on its size?
- Is 'n' always a non-negative integer, or should I handle cases where n is zero or negative?
- Can you confirm that the question is asking for the number of bulbs that are 'on' after 'n' rounds?
- If n is zero, should I return 0, or is there any other specified return value for an empty input?
- Are there any specific memory constraints I should be aware of when dealing with a large number of bulbs?
Brute Force Solution
Approach
Imagine you have a row of light bulbs, all initially off. The brute force strategy involves simulating each round of switching bulbs on or off, one by one, exactly as described in the problem.
Here's how the algorithm would work step-by-step:
- Start with all light bulbs switched off.
- Go through each round, from round one up to the total number of bulbs.
- In each round, visit every bulb and check if the bulb's number is divisible by the current round number.
- If it is, switch the bulb: if it's on, turn it off; if it's off, turn it on.
- After simulating all rounds, count how many bulbs are left on. That's the answer.
Code Implementation
def bulb_switcher_brute_force(number_of_bulbs):
bulbs = [False] * number_of_bulbs
for round_number in range(1, number_of_bulbs + 1):
for bulb_index in range(number_of_bulbs):
# Simulate each round, switching the appropriate bulbs.
if (bulb_index + 1) % round_number == 0:
bulbs[bulb_index] = not bulbs[bulb_index]
bulbs_on = 0
# Counting the number of bulbs switched on.
for bulb_status in bulbs:
if bulb_status:
bulbs_on += 1
return bulbs_onBig(O) Analysis
Optimal Solution
Approach
Instead of simulating every round of switching bulbs, the key is to recognize a pattern in which bulbs are toggled. A bulb ends up 'on' if it has been toggled an odd number of times, and this depends on the number of factors it has. The problem boils down to counting perfect squares.
Here's how the algorithm would work step-by-step:
- Understand that a bulb's final state (on or off) depends on how many times it's been switched.
- Realize that a bulb is switched once for each of its factors (numbers that divide evenly into it).
- Notice that most numbers have an even number of factors because factors come in pairs (e.g., for 12, 2 and 6 are a pair).
- Recognize that only perfect squares (numbers that are the result of squaring another number) have an odd number of factors (e.g., for 9, 3 is paired with itself).
- Therefore, count how many perfect squares are less than or equal to the total number of bulbs. This count will be the number of 'on' bulbs.
Code Implementation
def bulb_switcher(number_of_bulbs):
# Only perfect squares have an odd number of factors.
# Count perfect squares <= number_of_bulbs
count_of_on_bulbs = 0
current_perfect_square = 1
square_root = 1
while current_perfect_square <= number_of_bulbs:
count_of_on_bulbs += 1
square_root += 1
# Increment to the next perfect square.
current_perfect_square = square_root * square_root
return count_of_on_bulbsBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Input n is zero | Return 0, as there are no bulbs to switch. |
| Input n is a negative number | Return 0, as the number of bulbs cannot be negative; alternatively, throw an IllegalArgumentException to indicate invalid input. |
| Input n is 1 | Return 1, as the first bulb is always on. |
| Large input n, causing potential integer overflow if using iterative simulation | Use the mathematical solution (sqrt(n)) to avoid time complexity and potential overflow issues. |
| Integer overflow when calculating the square root for extremely large n. | Use a data type with sufficient range, like long, to represent the square root result or consider using a big integer library if the range of long is insufficient. |
| The `sqrt` function used may not be perfectly accurate due to floating-point representation | Cast `sqrt(n)` to an integer, this inherently truncates towards zero and is the correct behavior for this problem, but testing for corner cases like n = max integer is useful. |
| Non-integer input for n | Cast input to integer; Alternatively, throw an IllegalArgumentException to indicate invalid input, as problem description specifies integer n. |
| Edge case where sqrt(n) could have a very small fractional part | Casting the result of `sqrt(n)` to an integer correctly truncates the fractional part, giving the number of perfect squares less than or equal to n. |