Check if the Rectangle Corner Is Reachable

Hard

Asked by:

17 views

Topics:

GraphsArrays

You are given two positive integers xCorner and yCorner, and a 2D array circles, where circles[i] = [x_i, y_i, r_i] denotes a circle with center at (x_i, y_i) and radius r_i.

There is a rectangle in the coordinate plane with its bottom left corner at the origin and top right corner at the coordinate (xCorner, yCorner). You need to check whether there is a path from the bottom left corner to the top right corner such that the entire path lies inside the rectangle, does not touch or lie inside any circle, and touches the rectangle only at the two corners.

Return true if such a path exists, and false otherwise.

Example 1:

Input: xCorner = 3, yCorner = 4, circles = [[2,1,1]]

Output: true

Explanation:

The black curve shows a possible path between (0, 0) and (3, 4).

Example 2:

Input: xCorner = 3, yCorner = 3, circles = [[1,1,2]]

Output: false

Explanation:

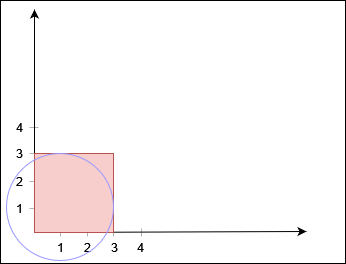
No path exists from (0, 0) to (3, 3).

Example 3:

Input: xCorner = 3, yCorner = 3, circles = [[2,1,1],[1,2,1]]

Output: false

Explanation:

No path exists from (0, 0) to (3, 3).

Example 4:

Input: xCorner = 4, yCorner = 4, circles = [[5,5,1]]

Output: true

Explanation:

Constraints:

3 <= xCorner, yCorner <= 10⁹
1 <= circles.length <= 1000
circles[i].length == 3
1 <= x_i, y_i, r_i <= 10⁹

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

Can you clarify the coordinate system used for the rectangle and the point? Is the origin at the bottom-left, and are the coordinates integers?
What are the possible ranges for the rectangle's dimensions (width and height) and the coordinates of the bottom-left corner and the target point? Can the rectangle have zero width or height?
Is the target point guaranteed to be within the same plane as the rectangle, or could it be significantly far away?
By 'reachable,' do you mean that it's possible to draw a straight line from the rectangle's bottom-left corner to the target point without intersecting the rectangle's interior (only edges and corners are allowed to intersect)?
If the target point is exactly the same as the bottom-left corner of the rectangle, should I return true or false?

Brute Force Solution

Approach

The brute force approach to this problem is to consider all possible paths from the starting point. We'll repeatedly try moving in all allowed directions until we either reach the target corner or hit a dead end.

Here's how the algorithm would work step-by-step:

Start at the initial position within the rectangle.
From the current position, explore every possible move based on the given constraints (for example, moving a certain distance horizontally or vertically).
For each possible move, check if that move takes us to the target corner. If so, we have found a solution and can stop.
If a move doesn't take us to the target, mark the new position as visited to avoid repeating paths and creating loops.
Continue exploring all possible moves from this new position, repeating steps 2-4.
If we reach a point where we cannot make any valid moves (we hit a boundary or a previously visited position), backtrack to the previous position and try a different move from there.
If we have exhausted all possible paths without finding the target corner, then the target is unreachable.

Code Implementation

def is_rectangle_corner_reachable(
        rectangle_width,
        rectangle_height,
        start_x,
        start_y,
        move_x,
        move_y):

    target_x = rectangle_width
    target_y = rectangle_height
    visited = set()

    def explore(current_x, current_y):
        # Base case: Reached the target
        if current_x == target_x and current_y == target_y:
            return True

        # Check if the current position has already been visited
        if (current_x, current_y) in visited:
            return False

        visited.add((current_x, current_y))

        # Define possible moves
        moves = [
            (current_x + move_x, current_y),
            (current_x - move_x, current_y),
            (current_x, current_y + move_y),
            (current_x, current_y - move_y)
        ]

        # Iterate through possible moves
        for next_x, next_y in moves:
            # Validate move:
            if 0 <= next_x <= rectangle_width and \
               0 <= next_y <= rectangle_height:

                # Recursively explore from the new position
                if explore(next_x, next_y):
                    return True

        # If no path found from here, backtrack
        return False

    # Begin search
    return explore(start_x, start_y)

Big(O) Analysis

Time Complexity

O(4^(m*n)) – The brute force approach explores all possible paths within the m x n rectangle. At each step, we can potentially move in up to four directions (though constraints might reduce that). In the worst-case scenario, we could repeatedly explore positions already visited, leading to an exponential number of paths. The number of possible paths is proportional to 4 raised to the power of the number of steps, which in the worst case could be related to the total area of the rectangle (m*n), so the overall complexity is O(4^(m*n)).

Space Complexity

O(M * N) – The brute force approach, as described, utilizes recursion and a visited set. The maximum depth of the recursion is bounded by the number of cells in the rectangle, represented as M * N, where M is the number of rows and N is the number of columns. In addition, to avoid revisiting cells, a visited set (or similar data structure) is needed to store the coordinates of cells already explored, which in the worst case, could also contain up to M * N elements. Therefore, the space complexity is driven by both the recursion stack and the visited set, leading to O(M * N) auxiliary space.

Optimal Solution

Approach

The core idea is to determine if the destination corner can be reached using only moves that are multiples of given dimensions. This involves understanding a property related to the greatest common divisor (GCD) of the rectangle's dimensions.

Here's how the algorithm would work step-by-step:

First, calculate the greatest common divisor (GCD) of the rectangle's width and height.
Then, check if both the x and y coordinates of the corner are evenly divisible by this GCD.
If both coordinates are divisible by the GCD, then the corner is reachable; otherwise, it is not.

Code Implementation

def check_if_rectangle_corner_is_reachable(rectangle_width, rectangle_height, corner_x, corner_y):    def calculate_greatest_common_divisor(first_number, second_number):        while(second_number):            first_number, second_number = second_number, first_number % second_number
        return first_number
    # Calculate the GCD of the rectangle's dimensions.
    greatest_common_divisor = calculate_greatest_common_divisor(rectangle_width, rectangle_height)

    # Check if the corner coordinates are divisible by the GCD.
    if corner_x % greatest_common_divisor == 0 and corner_y % greatest_common_divisor == 0:
        return True
    else:
        return False

Big(O) Analysis

Time Complexity

O(log(min(width, height))) – The dominant operation is calculating the greatest common divisor (GCD) of the rectangle's width and height. The Euclidean algorithm, commonly used for GCD calculation, has a time complexity of O(log(min(a, b))), where a and b are the two numbers. The remaining steps, checking divisibility by the GCD, are constant time operations. Therefore, the overall time complexity is determined by the GCD calculation, resulting in O(log(min(width, height))). The input size is reflected in the magnitudes of the width and height.

Space Complexity

O(1) – The algorithm calculates the greatest common divisor (GCD) and checks divisibility. These operations involve only a few integer variables to store intermediate calculations like the GCD itself and remainders. The number of variables used does not depend on the size of the input rectangle (width and height). Therefore, the auxiliary space used is constant.

Edge Cases

Case	How to Handle
Rectangle with zero width or height	Return true if both startX and startY are already 0, otherwise false, as the corner is reachable only at the origin.
Negative dx or dy values	Take the absolute values of dx and dy since direction doesn't affect reachability.
startX and startY are larger than the rectangle dimensions	Reduce startX and startY modulo the rectangle width and height, respectively, to work within bounds.
gcd(dx, width) == 0 and startX != 0	The x coordinate cannot be reached and should return false
gcd(dy, height) == 0 and startY != 0	The y coordinate cannot be reached and should return false
Large width, height, dx, dy values (potential overflow)	Use appropriate data types (e.g., long) to avoid integer overflow during calculations of gcd or modulo operations.
startX and startY are 0	Return true immediately as the corner is already at the origin.
Width and height are equal to dx and dy, respectively.	Reduce startX and startY using modulo to get the equivalent position within a single repetition of the rectangle's pattern.

Rectangle with zero width or height

How to Handle:

Return true if both startX and startY are already 0, otherwise false, as the corner is reachable only at the origin.

Negative dx or dy values

How to Handle:

Take the absolute values of dx and dy since direction doesn't affect reachability.

startX and startY are larger than the rectangle dimensions

How to Handle:

Reduce startX and startY modulo the rectangle width and height, respectively, to work within bounds.

gcd(dx, width) == 0 and startX != 0

How to Handle:

The x coordinate cannot be reached and should return false

gcd(dy, height) == 0 and startY != 0

How to Handle:

The y coordinate cannot be reached and should return false

Large width, height, dx, dy values (potential overflow)

How to Handle:

Use appropriate data types (e.g., long) to avoid integer overflow during calculations of gcd or modulo operations.

startX and startY are 0

How to Handle:

Return true immediately as the corner is already at the origin.

Width and height are equal to dx and dy, respectively.

How to Handle:

Reduce startX and startY using modulo to get the equivalent position within a single repetition of the rectangle's pattern.