Check if There Is a Valid Parentheses String Path

Hard

Asked by:

6 views

Topics:

ArraysDynamic Programming

A parentheses string is a non-empty string consisting only of '(' and ')'. It is valid if any of the following conditions is true:

It is ().
It can be written as AB (A concatenated with B), where A and B are valid parentheses strings.
It can be written as (A), where A is a valid parentheses string.

You are given an m x n matrix of parentheses grid. A valid parentheses string path in the grid is a path satisfying all of the following conditions:

The path starts from the upper left cell (0, 0).
The path ends at the bottom-right cell (m - 1, n - 1).
The path only ever moves down or right.
The resulting parentheses string formed by the path is valid.

Return true if there exists a valid parentheses string path in the grid. Otherwise, return false.

Example 1:

Input: grid = [["(","(","("],[")","(",")"],["(","(",")"],["(","(",")"]]
Output: true
Explanation: The above diagram shows two possible paths that form valid parentheses strings.
The first path shown results in the valid parentheses string "()(())".
The second path shown results in the valid parentheses string "((()))".
Note that there may be other valid parentheses string paths.

Example 2:

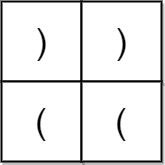
Input: grid = [[")",")"],["(","("]]
Output: false
Explanation: The two possible paths form the parentheses strings "))(" and ")((". Since neither of them are valid parentheses strings, we return false.

Constraints:

m == grid.length
n == grid[i].length
1 <= m, n <= 100
grid[i][j] is either '(' or ')'.

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the dimensions of the matrix, and what are the upper bounds for the number of rows and columns?
Can the matrix be empty (0x0)? What should I return in that case?
Besides '(' and ')', can the matrix contain any other characters?
What constitutes a 'valid parentheses string path'? Is it simply a path from the top-left to the bottom-right where at each step, the resulting string formed by concatenating the characters along the path is a valid parentheses string, and how do I define what a 'valid parentheses string' is?
If there are multiple valid paths, should I return true as soon as I find one, or do I need to find all of them (or return a specific one)?
Is diagonal movement allowed?

Brute Force Solution

Approach

The brute force way to solve this is to try every single possible path through the grid. We'll check if each of these paths creates a valid string of parentheses.

Here's how the algorithm would work step-by-step:

Start at the top-left corner of the grid.
Explore every possible path from the starting point to the bottom-right corner.
At each step, we can only move down or to the right.
As we follow each path, build a string by adding the parenthesis we encounter at each cell.
Once we reach the bottom-right corner, check if the string we built has balanced parentheses (meaning every open parenthesis has a matching close parenthesis in the correct order).
If we find at least one path that leads to a valid balanced string, then the answer is yes.
If we have explored every possible path and found no valid string, the answer is no.

Code Implementation

def check_if_there_is_a_valid_parentheses_string_path(grid):
    number_of_rows = len(grid)
    number_of_columns = len(grid[0])

    def is_valid_parentheses_string(parentheses_string):
        balance = 0
        for character in parentheses_string:
            if character == '(': 
                balance += 1
            else:
                balance -= 1
            if balance < 0:
                return False
        return balance == 0

    def find_path(row, column, current_string):
        # If we are out of bounds, this is not a valid path
        if row >= number_of_rows or column >= number_of_columns:
            return False

        current_string += grid[row][column]

        # We have reached the destination
        if row == number_of_rows - 1 and column == number_of_columns - 1:
            return is_valid_parentheses_string(current_string)

        # Explore going down
        if find_path(row + 1, column, current_string):
            return True

        # Explore going right
        if find_path(row, column + 1, current_string):
            return True

        return False

    # Initiate search from top-left
    return find_path(0, 0, '')

Big(O) Analysis

Time Complexity

O(2^(m+n)) – The algorithm explores every possible path from the top-left to the bottom-right corner of an m x n grid, where we can only move down or right. The number of paths is equivalent to choosing m moves down out of a total of m+n moves, or (m+n) choose m. In the worst case, where m and n are roughly equal, this is approximately 2^(m+n) since each cell gives us two options. Additionally, checking the validity of each path's parenthesis string of length m+n takes O(m+n) time. Therefore, the total time complexity is dominated by the exponential number of paths, leading to O(2^(m+n)).

Space Complexity

O(N) – The brute force approach explores every possible path from the top-left to the bottom-right corner using recursion. Each recursive call adds a stack frame, and in the worst case, a path can traverse all cells in the grid, where N is the total number of cells (rows * cols). Furthermore, a string of parentheses is built along each path, potentially reaching length N in the worst case. Therefore, the space complexity is dominated by the maximum recursion depth and the string's size, both of which can be proportional to N.

Optimal Solution

Approach

The core idea is to use a technique to efficiently explore all possible paths in the grid, keeping track of the balance between open and closed parentheses. If we reach the destination with a balanced state (equal number of open and closed parentheses), it means we have found a valid path. We avoid recomputing paths by remembering previously visited locations and their parenthesis balance.

Here's how the algorithm would work step-by-step:

Begin at the starting point of the grid and maintain a count to represent the running balance of open and closed parentheses as you move along a path.
At each position in the grid, update the parenthesis count. Add one for an open parenthesis and subtract one for a closed parenthesis.
To prevent re-exploration of the same paths and avoid exceeding limits of the environment, store information about each grid position and the parenthesis count at that position to remember the state.
If at any point the parenthesis count goes below zero, this indicates an invalid path because there are more closed parentheses than open ones. Discard this path immediately.
Continue exploring paths recursively or iteratively. When a path reaches the end point, verify if the parenthesis count is zero. If it is, a valid path exists and the process may stop (if we need just one valid path).
If all paths are explored and no valid path with a final parenthesis count of zero is discovered, then no valid path exists.

Code Implementation

def check_if_there_is_a_valid_parentheses_string_path(grid):
    number_of_rows = len(grid)
    number_of_columns = len(grid[0])

    # Use a set to store visited states (row, col, balance).
    visited = set()

    def depth_first_search(row, col, parenthesis_balance):
        # If out of bounds, return False
        if row < 0 or row >= number_of_rows or col < 0 or col >= number_of_columns:
            return False

        # Update the parenthesis balance.
        if grid[row][col] == '(': 
            parenthesis_balance += 1
        else:
            parenthesis_balance -= 1

        # If balance is negative, it's invalid.
        if parenthesis_balance < 0:
            return False

        # If we reached the destination.
        if row == number_of_rows - 1 and col == number_of_columns - 1:
            # Valid path if the parenthesis are balanced
            return parenthesis_balance == 0

        # Check if the state has been visited before
        if (row, col, parenthesis_balance) in visited:
            return False

        # Mark the current state as visited.
        visited.add((row, col, parenthesis_balance))

        # Explore the path downwards and to the right
        down = depth_first_search(row + 1, col, parenthesis_balance)
        right = depth_first_search(row, col + 1, parenthesis_balance)

        return down or right

    # Initiate dfs with the top-left cell
    return depth_first_search(0, 0, 0)

Big(O) Analysis

Time Complexity

O(m * n * (m + n)) – Let m and n be the dimensions of the grid. The algorithm explores paths in the grid, and in the worst case, it might visit each cell multiple times with different parenthesis balance values. The parenthesis balance can range from -(m+n) to (m+n) (though it will never be negative due to the early termination), but we are mainly bound by the positive range up to m+n. Therefore, we can explore each of the m * n cells up to m+n times. This means the time complexity is O(m * n * (m + n)), where (m+n) is the range of possible open parenthesis count at each cell.

Space Complexity

O(M * N * K) – The space complexity is determined by the memoization used to store information about visited grid positions and their parenthesis count. We have a grid of size M x N, and for each cell, we store the parenthesis count. The parenthesis count can range from -K to K, but since we discard paths with negative counts, the maximum count is K, where K is the maximum possible parenthesis imbalance (worst case being all open parentheses). Thus, we have to store a memo of size M * N * (K+1) which simplifies to O(M * N * K).

Edge Cases

Case	How to Handle
Null or empty grid	Return false immediately, as there's no path to traverse.
Grid with only one cell	Return true if the single cell contains a parenthesis, otherwise false.
Grid with mismatched starting/ending parentheses	If the starting cell is ')' or the ending cell is '(', a valid path is impossible, so return false.
Long path exceeding maximum recursion depth (if using recursion)	Use dynamic programming (memoization) or iterative approach to avoid stack overflow errors.
Grid containing non-parenthesis characters	Treat non-parenthesis characters as invalid input and return false.
No valid path exists despite balanced parentheses in the grid	The algorithm should explore all possible paths and correctly return false if no valid path exists.
Large grid dimensions impacting memory usage	Optimize memory usage by using techniques like bitmasking to represent the parenthesis balance, or using an in-place modification approach if allowed and feasible.
Grid with only opening or only closing parentheses preventing balance	The path will never become balanced, leading to no valid path and return false.

Null or empty grid

How to Handle:

Return false immediately, as there's no path to traverse.

Grid with only one cell

How to Handle:

Return true if the single cell contains a parenthesis, otherwise false.

Grid with mismatched starting/ending parentheses

How to Handle:

If the starting cell is ')' or the ending cell is '(', a valid path is impossible, so return false.

Long path exceeding maximum recursion depth (if using recursion)

How to Handle:

Use dynamic programming (memoization) or iterative approach to avoid stack overflow errors.

Grid containing non-parenthesis characters

How to Handle:

Treat non-parenthesis characters as invalid input and return false.

No valid path exists despite balanced parentheses in the grid

How to Handle:

The algorithm should explore all possible paths and correctly return false if no valid path exists.

Large grid dimensions impacting memory usage

How to Handle:

Optimize memory usage by using techniques like bitmasking to represent the parenthesis balance, or using an in-place modification approach if allowed and feasible.

Grid with only opening or only closing parentheses preventing balance

How to Handle:

The path will never become balanced, leading to no valid path and return false.