Count Total Number of Colored Cells
MediumThere exists an infinitely large two-dimensional grid of uncolored unit cells. You are given a positive integer n, indicating that you must do the following routine for n minutes:
- At the first minute, color any arbitrary unit cell blue.
- Every minute thereafter, color blue every uncolored cell that touches a blue cell.
Below is a pictorial representation of the state of the grid after minutes 1, 2, and 3.
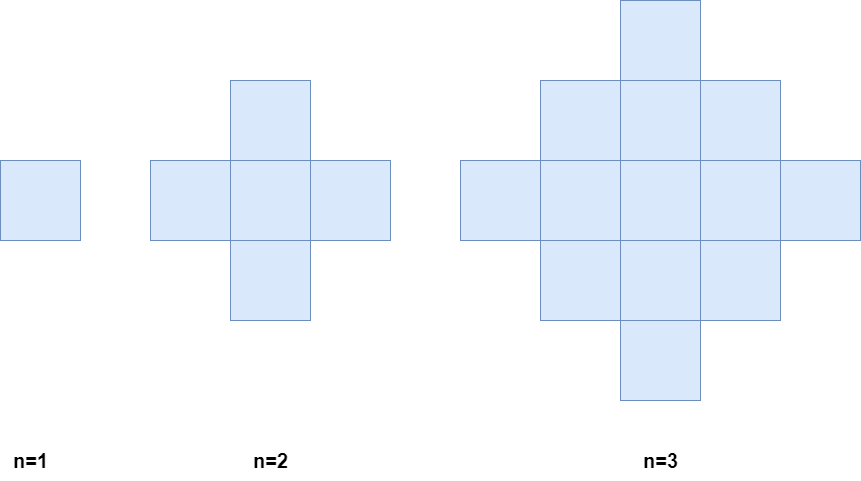
Return the number of colored cells at the end of n minutes.
Example 1:
Input: n = 1 Output: 1 Explanation: After 1 minute, there is only 1 blue cell, so we return 1.
Example 2:
Input: n = 2 Output: 5 Explanation: After 2 minutes, there are 4 colored cells on the boundary and 1 in the center, so we return 5.
Constraints:
1 <= n <= 105
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the maximum possible value for `n`? I want to be mindful of potential integer overflow issues.
- Can `n` be zero or negative?
- By 'colored cells', do you mean all cells within the outermost square, or just the cells that are part of the concentric squares themselves (i.e., the cells that form the perimeter of each square)?
- Is there a specific return type expected (e.g., `int`, `long`)?
- Could you provide a small example (e.g., n=3) and the corresponding expected output to ensure I fully understand the problem?
Brute Force Solution
Approach
The brute force way to count colored cells involves simulating the coloring process step-by-step. We'll essentially 'draw' the grid for each size increment and count the colored cells directly. This method guarantees finding the answer by explicitly constructing the pattern.
Here's how the algorithm would work step-by-step:
- Start with a completely empty grid.
- For the first step (size 1), color the single center cell.
- For the next step (size 2), color the appropriate cells around the existing colored cells to expand the pattern.
- Count all the colored cells in the grid at this step.
- Repeat the coloring and counting process for each subsequent step, always building upon the colored cells from the previous step.
- Continue this process until you reach the desired size.
- The final count of colored cells is your answer.
Code Implementation
def count_colored_cells_brute_force(size):
grid_dimension = 2 * size - 1
grid = [[0] * grid_dimension for _ in range(grid_dimension)]
center_row = size - 1
center_column = size - 1
grid[center_row][center_column] = 1
total_colored_cells = 1
for current_size in range(2, size + 1):
# Expand the colored cells outwards from the center
for i in range(center_row - (current_size - 1), center_row + current_size):
if 0 <= i < grid_dimension and grid[i][center_column - (current_size - 1)] == 0:
grid[i][center_column - (current_size - 1)] = 1
total_colored_cells += 1
for i in range(center_row - (current_size - 1), center_row + current_size):
if 0 <= i < grid_dimension and grid[i][center_column + (current_size - 1)] == 0:
grid[i][center_column + (current_size - 1)] = 1
total_colored_cells += 1
for j in range(center_column - (current_size - 2), center_column + (current_size - 1)):
if 0 <= j < grid_dimension and grid[center_row - (current_size - 1)][j] == 0:
grid[center_row - (current_size - 1)][j] = 1
total_colored_cells += 1
for j in range(center_column - (current_size - 2), center_column + (current_size - 1)):
if 0 <= j < grid_dimension and grid[center_row + (current_size - 1)][j] == 0:
grid[center_row + (current_size - 1)][j] = 1
total_colored_cells += 1
return total_colored_cellsBig(O) Analysis
Optimal Solution
Approach
The most efficient way to count colored cells is to recognize a pattern that emerges as the size increases. Instead of simulating the cell coloring process, we leverage this pattern to directly calculate the number of colored cells.
Here's how the algorithm would work step-by-step:
- Observe that the number of colored cells follows a pattern related to squares.
- Specifically, realize that for a given size, the total number of colored cells can be calculated using a simple formula involving squaring the size and then adjusting it.
- The size of the board can be plugged directly into the derived formula to get the result.
- Apply the formula to determine the total number of colored cells efficiently.
Code Implementation
def count_colored_cells(size):
# For size 1, only 1 cell is colored.
if size == 1:
return 1
# The total number of colored cells is size * size + (size - 1) * (size - 1)
total_colored_cells = size * size + (size - 1) * (size - 1)
return total_colored_cells
def count_total_number_colored_cells(size_of_board):
# If the size is 0 or negative, there are no colored cells
if size_of_board <= 0:
return 0
# Formula: n^2 + (n-1)^2 = 2n^2 - 2n + 1
total_colored_cells = 2 * size_of_board * size_of_board - 2 * size_of_board + 1
# Return the calculated number of colored cells.
return total_colored_cellsBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| n is zero | Return 0 as there are no squares and thus no colored cells. |
| n is one | Return 1, corresponding to the single colored cell of the innermost square. |
| Large value of n that could lead to integer overflow | Use a larger integer type (e.g., long) to avoid potential overflow during calculation. |
| Negative input | Throw an IllegalArgumentException or return an error value because the number of squares cannot be negative. |
| Maximum integer value for n | Check for possible overflow issues when computing `(2 * n * n) - (2 * n) + 1`, possibly requiring arbitrary-precision arithmetic. |
| n is close to the maximum integer value, where n^2 might overflow. | Use long long or a language that supports large integers. |
| n is a very large number, leading to memory issues | The formula-based solution has a constant memory footprint and handles arbitrarily large n (within the data type limits). |
| The calculated value might exceed the maximum value representable by the integer type. | Use a long integer to avoid integer overflow issues. |