Dungeon Game

Hard

Asked by:

34 views

Topics:

Dynamic Programming

The demons had captured the princess and imprisoned her in the bottom-right corner of a dungeon. The dungeon consists of m x n rooms laid out in a 2D grid. Our valiant knight was initially positioned in the top-left room and must fight his way through dungeon to rescue the princess.

The knight has an initial health point represented by a positive integer. If at any point his health point drops to 0 or below, he dies immediately.

Some of the rooms are guarded by demons (represented by negative integers), so the knight loses health upon entering these rooms; other rooms are either empty (represented as 0) or contain magic orbs that increase the knight's health (represented by positive integers).

To reach the princess as quickly as possible, the knight decides to move only rightward or downward in each step.

Return the knight's minimum initial health so that he can rescue the princess.

Note that any room can contain threats or power-ups, even the first room the knight enters and the bottom-right room where the princess is imprisoned.

Example 1:

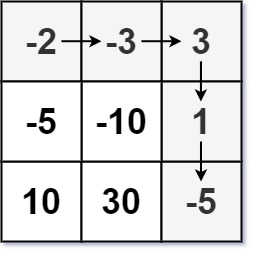
Input: dungeon = [[-2,-3,3],[-5,-10,1],[10,30,-5]]
Output: 7
Explanation: The initial health of the knight must be at least 7 if he follows the optimal path: RIGHT-> RIGHT -> DOWN -> DOWN.

Example 2:

Input: dungeon = [[0]]
Output: 1

Constraints:

m == dungeon.length
n == dungeon[i].length
1 <= m, n <= 200
-1000 <= dungeon[i][j] <= 1000

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

Can the dungeon have negative values, zero values, or only positive values?
What are the dimensions' constraints for the dungeon grid (rows and columns)?
What is the minimum initial health the knight starts with? Can it be assumed to be 1?
If the knight's health drops to zero or below at any point, is the dungeon un-winnable?
If there are multiple paths that require the same minimum initial health, is any one acceptable?

Brute Force Solution

Approach

The brute force way to solve this dungeon problem is to explore every single possible path the hero could take through the dungeon. We want to find the path that requires the least initial health to survive. We'll try every route and see what happens.

Here's how the algorithm would work step-by-step:

Start at the beginning of the dungeon with some amount of initial health.
Try going right and see if the hero survives. Then, starting from the beginning again with the same initial health, try going down.
If the hero survives going right, explore all possible paths from that new spot. Similarly, if the hero survives going down, explore all paths from there.
Keep track of the initial health needed for each path that allows the hero to reach the end of the dungeon alive.
If the hero runs out of health at any point along a path, that path is a failure, and we discard it.
Repeat this process with different amounts of initial health until we find the lowest possible initial health that allows at least one path to succeed.
The lowest initial health needed to complete the dungeon is the answer.

Code Implementation

def calculate_minimum_initial_health(dungeon):
    number_of_rows = len(dungeon)
    number_of_columns = len(dungeon[0])

    def explore_path(current_row, current_column, current_health, initial_health_needed):
        current_health += dungeon[current_row][current_column]

        if current_health <= 0:
            return float('inf')

        if current_row == number_of_rows - 1 and current_column == number_of_columns - 1:
            return initial_health_needed

        minimum_health_needed = float('inf')

        # Explore the path going right
        if current_column + 1 < number_of_columns:

            minimum_health_needed = min(minimum_health_needed, \
                explore_path(current_row, current_column + 1, current_health, initial_health_needed))

        # Explore the path going down
        if current_row + 1 < number_of_rows:

            minimum_health_needed = min(minimum_health_needed, \
                explore_path(current_row + 1, current_column, current_health, initial_health_needed))

        return minimum_health_needed

    minimum_initial_health = float('inf')
    initial_health = 1

    # Brute force: try every initial health value until we find the minimum
    while initial_health < 201:
        health_needed_for_path = explore_path(0, 0, 0, initial_health)

        #Keep track of best possible health
        minimum_initial_health = min(minimum_initial_health, health_needed_for_path)
        initial_health += 1

    return minimum_initial_health

Big(O) Analysis

Time Complexity

O(2^(m+n)) – The described brute force approach explores every possible path through the dungeon. In an m x n dungeon, a path from the top-left to the bottom-right can involve up to m-1 downward moves and n-1 rightward moves. At each cell, the algorithm potentially branches into two choices (right or down), leading to an exponential number of paths explored. Thus, the number of paths grows on the order of 2 to the power of the sum of m and n, which can be approximated as O(2^(m+n)).

Space Complexity

O(m*n) – The brute force approach explores every possible path through the m x n dungeon using recursion. In the worst-case scenario, the recursion depth can reach m*n, where m is the number of rows and n is the number of columns in the dungeon, representing the total number of cells. Each recursive call requires space on the call stack to store function arguments and local variables. Therefore, the maximum auxiliary space used by the recursion stack is proportional to the number of cells in the dungeon. This results in a space complexity of O(m*n).

Optimal Solution

Approach

The goal is to find the minimum health needed to successfully navigate a dungeon. We work backward from the end to the start, figuring out the minimum health needed at each step to survive.

Here's how the algorithm would work step-by-step:

Imagine you're at the destination. You need at least 1 health point to survive there.
Now, look at the cells directly before the destination (above and to the left). Figure out how much health you need in those cells to reach the destination with at least 1 health.
Keep going backward, one cell at a time. For each cell, figure out the minimum health you need to enter that cell, considering the health you'll gain or lose in that cell and the minimum health needed in the best next step (either down or right).
The best next step is the one that requires the least amount of starting health.
Continue this process until you reach the starting cell. The health value you calculate for the starting cell is the minimum initial health needed to survive the entire dungeon.

Code Implementation

def calculate_minimum_hp(dungeon):
    rows = len(dungeon)
    cols = len(dungeon[0])

    # Initialize the health points matrix with default values
    health_points = [[0] * cols for _ in range(rows)]

    # Start from the end cell and work backwards
    for row_index in range(rows - 1, -1, -1):
        for col_index in range(cols - 1, -1, -1):
            if row_index == rows - 1 and col_index == cols - 1:
                health_points[row_index][col_index] = max(1, 1 - dungeon[row_index][col_index])
            else:
                # Determine minimum health needed from the next possible moves
                down_health = health_points[row_index + 1][col_index] if row_index + 1 < rows else float('inf')
                right_health = health_points[row_index][col_index + 1] if col_index + 1 < cols else float('inf')

                min_next_health = min(down_health, right_health)

                # We need to ensure survival in current cell too
                health_points[row_index][col_index] = max(1, min_next_health - dungeon[row_index][col_index])

    # Minimum health needed at start position is the final result
    return health_points[0][0]

Big(O) Analysis

Time Complexity

O(m*n) – The algorithm iterates through each cell in the dungeon exactly once, working backward from the destination to the starting point. The dungeon is represented as a 2D grid with dimensions m rows and n columns. Therefore, the algorithm visits each of the m*n cells in the grid. Since the operations performed at each cell (calculating the minimum health needed) take constant time, the overall time complexity is proportional to the number of cells, which is m*n.

Space Complexity

O(m * n) – The algorithm uses a 2D array (or matrix) of the same dimensions as the dungeon (m rows and n columns) to store the minimum health needed at each cell. This array stores intermediate results as it works backward from the destination to the start. Thus, the auxiliary space required grows linearly with the number of cells in the dungeon. Therefore, the space complexity is O(m * n), where m is the number of rows and n is the number of columns in the dungeon.

Edge Cases

Case	How to Handle
Empty dungeon (null or zero-sized grid)	Return 1, as the minimum initial health required is always at least 1, according to the problem description.
Dungeon with only one cell (1x1 grid)	The minimum initial health should be calculated as max(1, 1 - dungeon[0][0]).
Dungeon with all positive values	The minimum initial health should be calculated based on the path with least positive gain, always resulting in a value <= 1.
Dungeon with all negative values	The minimum initial health can be very large, requiring appropriate integer handling to avoid overflows.
Dungeon with values that cause integer overflow when calculating health	Use long data type to store the intermediate health values to prevent integer overflow.
A path exists where the knight's health never drops below 1	The algorithm correctly calculates the minimum starting health as 1 in this scenario.
Dungeon with dimensions approaching maximum allowed (m, n <= 200)	The DP solution should still scale efficiently without exceeding time or memory limits.
The princess cell has a very large negative value	The algorithm correctly adjusts the minimum initial health to account for the large deficit at the end.

Empty dungeon (null or zero-sized grid)

How to Handle:

Return 1, as the minimum initial health required is always at least 1, according to the problem description.

Dungeon with only one cell (1x1 grid)

How to Handle:

The minimum initial health should be calculated as max(1, 1 - dungeon[0][0]).

Dungeon with all positive values

How to Handle:

The minimum initial health should be calculated based on the path with least positive gain, always resulting in a value <= 1.

Dungeon with all negative values

How to Handle:

The minimum initial health can be very large, requiring appropriate integer handling to avoid overflows.

Dungeon with values that cause integer overflow when calculating health

How to Handle:

Use long data type to store the intermediate health values to prevent integer overflow.

A path exists where the knight's health never drops below 1

How to Handle:

The algorithm correctly calculates the minimum starting health as 1 in this scenario.

Dungeon with dimensions approaching maximum allowed (m, n <= 200)

How to Handle:

The DP solution should still scale efficiently without exceeding time or memory limits.

The princess cell has a very large negative value

How to Handle:

The algorithm correctly adjusts the minimum initial health to account for the large deficit at the end.