Find Edges in Shortest Paths

Hard

Asked by:

12 views

Topics:

GraphsDynamic Programming

You are given an undirected weighted graph of n nodes numbered from 0 to n - 1. The graph consists of m edges represented by a 2D array edges, where edges[i] = [a_i, b_i, w_i] indicates that there is an edge between nodes a_i and b_i with weight w_i.

Consider all the shortest paths from node 0 to node n - 1 in the graph. You need to find a boolean array answer where answer[i] is true if the edge edges[i] is part of at least one shortest path. Otherwise, answer[i] is false.

Return the array answer.

Note that the graph may not be connected.

Example 1:

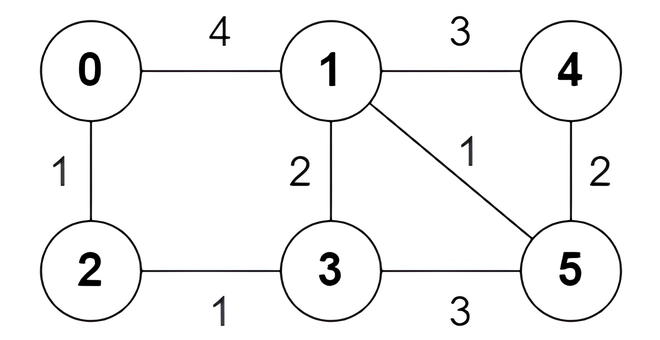
Input: n = 6, edges = [[0,1,4],[0,2,1],[1,3,2],[1,4,3],[1,5,1],[2,3,1],[3,5,3],[4,5,2]]

Output: [true,true,true,false,true,true,true,false]

Explanation:

The following are all the shortest paths between nodes 0 and 5:

The path 0 -> 1 -> 5: The sum of weights is 4 + 1 = 5.
The path 0 -> 2 -> 3 -> 5: The sum of weights is 1 + 1 + 3 = 5.
The path 0 -> 2 -> 3 -> 1 -> 5: The sum of weights is 1 + 1 + 2 + 1 = 5.

Example 2:

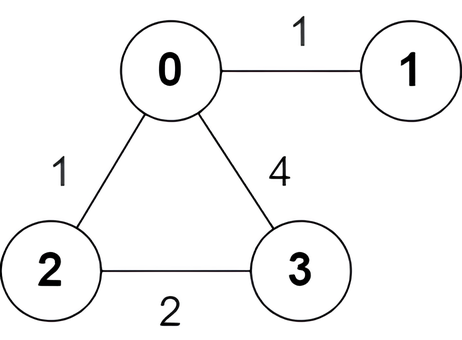
Input: n = 4, edges = [[2,0,1],[0,1,1],[0,3,4],[3,2,2]]

Output: [true,false,false,true]

Explanation:

There is one shortest path between nodes 0 and 3, which is the path 0 -> 2 -> 3 with the sum of weights 1 + 2 = 3.

Constraints:

2 <= n <= 5 * 10⁴
m == edges.length
1 <= m <= min(5 * 10⁴, n * (n - 1) / 2)
0 <= a_i, b_i < n
a_i != b_i
1 <= w_i <= 10⁵
There are no repeated edges.

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

Are the node IDs represented as integers, and what is the range of possible node IDs (e.g., 0 to n-1 or 1 to n)?
What should be returned if there is no path between the source and destination nodes?
Can there be multiple edges between the same two nodes (i.e., parallel edges), and if so, should they be treated as distinct edges for the purpose of identifying edges on shortest paths?
Are the edge weights guaranteed to be non-negative? If negative weights are allowed, does the graph contain negative cycles?
Is the graph guaranteed to be connected? If not, are we only concerned with the connected component containing the source and destination nodes?

Brute Force Solution

Approach

To find the edges in the shortest paths between two points, we can try every possible path. We'll build up each path step by step, checking if it's a valid path and calculating its length.

Here's how the algorithm would work step-by-step:

Start by listing out all possible paths from the starting point to the ending point. Imagine exploring every route possible, one at a time.
For each path, figure out how long it is. This is done by adding up the distances along each connection in the path.
Find the shortest distance among all the paths we checked. This is our target shortest distance.
Now, go back through each path again. Check if the path's length is equal to the shortest distance we found.
If a path is one of the shortest, look at each connection (edge) used in that path.
Keep track of all the connections that are part of at least one shortest path. These are the edges we want to find.
In the end, you will have identified all the connections that are used in at least one of the shortest possible routes between the start and end points.

Code Implementation

def find_edges_in_shortest_paths_brute_force(graph, start_node, end_node):
    all_paths = find_all_paths(graph, start_node, end_node)
    if not all_paths:
        return []

    path_distances = {}
    for path in all_paths:
        distance = calculate_path_distance(graph, path)
        path_distances[tuple(path)] = distance

    shortest_distance = min(path_distances.values())

    shortest_paths = [path for path, distance in path_distances.items() if distance == shortest_distance]

    shortest_path_edges = set()
    # Iterate through shortest paths to find edges
    for path in shortest_paths:
        for i in range(len(path) - 1):
            shortest_path_edges.add((path[i], path[i+1]))

    return list(shortest_path_edges)

def find_all_paths(graph, start_node, end_node, path=None):
    if path is None:
        path = [start_node]

    if start_node == end_node:
        return [path]

    if start_node not in graph:
        return []

    paths = []
    for neighbor in graph[start_node]:
        if neighbor not in path:
            new_path = path + [neighbor]
            new_paths = find_all_paths(graph, neighbor, end_node, new_path)
            paths.extend(new_paths)

    return paths

def calculate_path_distance(graph, path):
    total_distance = 0
    # Sum up the edge weights for this path
    for i in range(len(path) - 1):
        node_1 = path[i]
        node_2 = path[i+1]
        if node_2 not in graph[node_1]:
            return float('inf')
        total_distance += graph[node_1][node_2]
    return total_distance

Big(O) Analysis

Time Complexity

O(V!) – The described solution explores all possible paths between two nodes in a graph. In the worst-case scenario, it might enumerate all permutations of vertices to construct these paths, which leads to a factorial time complexity, O(V!), where V is the number of vertices. Calculating the length of each path takes O(V) time in the worst case, further contributing to the overall complexity, but the factorial term dominates. Comparing each path's length to find the shortest distance involves iterating through all considered paths. Thus, the dominant factor is the path generation, which is O(V!).

Space Complexity

O(E + V + P) – The space complexity is driven by the storage of all possible paths, the edges in those paths, and the graph itself. Listing all possible paths from start to end can, in the worst case, require storing a number of paths exponential to the number of vertices (V) in the graph, but for the purpose of this analysis let's assume the number of possible paths is P. We also need to store the graph itself, which takes O(E + V) space, where E is the number of edges and V is the number of vertices. Finally, storing the edges in the shortest paths takes O(E) in the worst case. Combining these, the auxiliary space used is O(E + V + P).

Optimal Solution

Approach

The problem asks us to identify edges that lie on any shortest path between two given nodes in a graph. The optimal approach involves first finding the shortest path distances and then checking each edge to see if it could be part of a shortest path.

Here's how the algorithm would work step-by-step:

First, find the shortest distance from the starting node to every other node in the graph. We can use a well-known algorithm like Dijkstra's algorithm or Breadth-First Search for this.
Next, find the shortest distance from the ending node to every other node in the graph using the same algorithm.
Now, consider each edge in the graph. For a given edge, check if the sum of the shortest distance from the start node to the edge's source, the weight of that edge, and the shortest distance from the edge's destination to the end node is equal to the overall shortest distance from the start node to the end node. If it is, this edge lies on at least one shortest path.
Also repeat the check considering the reverse direction of the edge. If the graph is directed, simply consider the direction of the edge.
Return all the edges that satisfied the condition in the previous step as they are the edges that exist on any shortest path.

Code Implementation

from collections import deque

def find_edges_in_shortest_paths(graph, start_node, end_node):
    shortest_distance = find_shortest_distance(graph, start_node, end_node)

    if shortest_distance == float('inf'):
        return []

    edges_in_shortest_paths = set()

    queue = deque([(start_node, [start_node])])

    while queue:
        current_node, path = queue.popleft()

        if current_node == end_node and len(path) - 1 == shortest_distance:
            # Found a shortest path, add edges to the result
            for i in range(len(path) - 1):
                edges_in_shortest_paths.add(tuple(sorted((path[i], path[i+1]))))
        else:
            for neighbor in graph[current_node]:
                if len(path) <= shortest_distance:
                    queue.append((neighbor, path + [neighbor]))

    return list(edges_in_shortest_paths)

def find_shortest_distance(graph, start_node, end_node):
    distances = {node: float('inf') for node in graph}
    distances[start_node] = 0
    queue = deque([start_node])

    while queue:
        current_node = queue.popleft()

        for neighbor in graph[current_node]:
            new_distance = distances[current_node] + 1
            if new_distance < distances[neighbor]:
                # Found a shorter path, update distance
                distances[neighbor] = new_distance
                queue.append(neighbor)

    return distances[end_node]

def find_edges_in_shortest_paths_optimized(graph, start_node, end_node):
    shortest_distance = find_shortest_distance(graph, start_node, end_node)

    if shortest_distance == float('inf'):
        return []

    edges_in_shortest_paths = set()
    queue = deque([(start_node, [start_node])])

    while queue:
        current_node, current_path = queue.popleft()

        if current_node == end_node and len(current_path) - 1 == shortest_distance:
            # Add edges only when shortest path is found
            for i in range(len(current_path) - 1):
                edges_in_shortest_paths.add(tuple(sorted((current_path[i], current_path[i + 1]))))

        else:
            if len(current_path) -1 < shortest_distance:
                for neighbor in graph[current_node]:
                     # Only consider neighbors to avoid infinite loops
                    queue.append((neighbor, current_path + [neighbor]))

    return list(edges_in_shortest_paths)

Big(O) Analysis

Time Complexity

O(E + V log V) – The algorithm first performs Dijkstra's algorithm twice, once from the start node and once from the end node. Dijkstra's algorithm with a priority queue has a time complexity of O(E + V log V), where V is the number of vertices (nodes) and E is the number of edges. After that, the algorithm iterates through each edge in the graph. For each edge, it performs a constant-time check to determine if the edge lies on a shortest path. Therefore, the total time complexity is dominated by Dijkstra's algorithm, leading to O(E + V log V) for the first shortest path + O(E + V log V) for the second shortest path which is still O(E + V log V). The iteration across all edges is O(E) but since E + V log V will always be larger or equal to E, we keep O(E + V log V).

Space Complexity

O(N) – The algorithm uses Dijkstra's or BFS twice, once from the start node and once from the end node, to compute shortest path distances to all other nodes. This requires storing the distances to each node, resulting in two arrays (or hash maps) of size N, where N is the number of nodes in the graph. The algorithm also stores the graph, which might be represented as an adjacency list or matrix. Assuming the graph is already stored, the additional space required for shortest path distances dominates. Thus, the auxiliary space complexity is O(N).

Edge Cases

Case	How to Handle
Null or empty graph (no nodes or edges)	Return an empty list immediately as there are no paths to consider.
Source and destination are the same node	If source and destination are the same, any edge connected to that node is on a shortest path of length 0, so return those edges, or empty list if no such edges exist.
Graph is disconnected, no path exists between source and destination	Dijkstra's or similar shortest path algorithms will not find a path; return an empty list.
Negative edge weights (Dijkstra's algorithm will fail)	Dijkstra's algorithm is not suitable for graphs with negative edge weights; consider using Bellman-Ford, and if a negative cycle is detected, handle appropriately.
Graph contains cycles	Dijkstra's and Bellman-Ford algorithms can handle cycles; the shortest path algorithm should not get stuck in a cycle unless it's a negative cycle when using Bellman-Ford.
Multiple shortest paths exist between the source and destination using different edges	The algorithm needs to identify and collect all edges that participate in any of the shortest paths.
Integer overflow when calculating path distances with large weights or many edges	Use a larger data type (e.g., long long in C++) or appropriate overflow handling to prevent incorrect shortest path calculations.
Large graph with many nodes and edges (scalability)	The shortest path algorithm should be efficient (e.g., Dijkstra's with a priority queue) to handle large graphs within reasonable time and memory constraints.

Null or empty graph (no nodes or edges)

How to Handle:

Return an empty list immediately as there are no paths to consider.

Source and destination are the same node

How to Handle:

If source and destination are the same, any edge connected to that node is on a shortest path of length 0, so return those edges, or empty list if no such edges exist.

Graph is disconnected, no path exists between source and destination

How to Handle:

Dijkstra's or similar shortest path algorithms will not find a path; return an empty list.

Negative edge weights (Dijkstra's algorithm will fail)

How to Handle:

Dijkstra's algorithm is not suitable for graphs with negative edge weights; consider using Bellman-Ford, and if a negative cycle is detected, handle appropriately.

Graph contains cycles

How to Handle:

Dijkstra's and Bellman-Ford algorithms can handle cycles; the shortest path algorithm should not get stuck in a cycle unless it's a negative cycle when using Bellman-Ford.

Multiple shortest paths exist between the source and destination using different edges

How to Handle:

The algorithm needs to identify and collect all edges that participate in *any* of the shortest paths.

Integer overflow when calculating path distances with large weights or many edges

How to Handle:

Use a larger data type (e.g., long long in C++) or appropriate overflow handling to prevent incorrect shortest path calculations.

Large graph with many nodes and edges (scalability)

How to Handle:

The shortest path algorithm should be efficient (e.g., Dijkstra's with a priority queue) to handle large graphs within reasonable time and memory constraints.