Find the Number of Distinct Colors Among the Balls

Medium

Asked by:

18 views

Topics:

Arrays

You are given an integer limit and a 2D array queries of size n x 2.

There are limit + 1 balls with distinct labels in the range [0, limit]. Initially, all balls are uncolored. For every query in queries that is of the form [x, y], you mark ball x with the color y. After each query, you need to find the number of colors among the balls.

Return an array result of length n, where result[i] denotes the number of colors after i^th query.

Note that when answering a query, lack of a color will not be considered as a color.

Example 1:

Input: limit = 4, queries = [[1,4],[2,5],[1,3],[3,4]]

Output: [1,2,2,3]

Explanation:

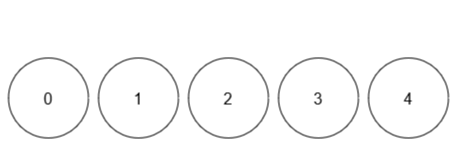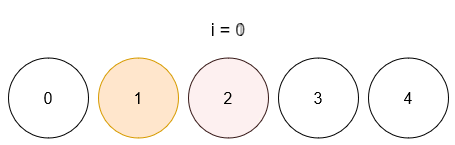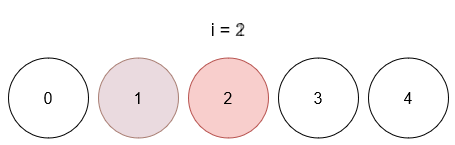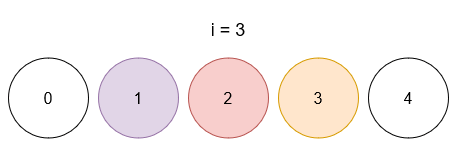
After query 0, ball 1 has color 4.
After query 1, ball 1 has color 4, and ball 2 has color 5.
After query 2, ball 1 has color 3, and ball 2 has color 5.
After query 3, ball 1 has color 3, ball 2 has color 5, and ball 3 has color 4.

Example 2:

Input: limit = 4, queries = [[0,1],[1,2],[2,2],[3,4],[4,5]]

Output: [1,2,2,3,4]

Explanation:

After query 0, ball 0 has color 1.
After query 1, ball 0 has color 1, and ball 1 has color 2.
After query 2, ball 0 has color 1, and balls 1 and 2 have color 2.
After query 3, ball 0 has color 1, balls 1 and 2 have color 2, and ball 3 has color 4.
After query 4, ball 0 has color 1, balls 1 and 2 have color 2, ball 3 has color 4, and ball 4 has color 5.

Constraints:

1 <= limit <= 10⁹
1 <= n == queries.length <= 10⁵
queries[i].length == 2
0 <= queries[i][0] <= limit
1 <= queries[i][1] <= 10⁹

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What is the range of possible values for the colors of the balls? Can I assume they are non-negative integers?
Is the input list guaranteed to be non-empty? What should I return if the input is null or empty?
Are the color values represented as integers? Could they be strings or another data type?
By 'distinct', do you mean unique color values only, or is the *number* of unique colors what I should return?
Is there an upper bound on the number of balls (the length of the input)? This will help me understand memory usage implications.

Brute Force Solution

Approach

The brute force approach to finding the number of distinct colors is straightforward. We will look at each ball one at a time and keep track of which colors we've already seen. By the end, we will know how many unique colors exist.

Here's how the algorithm would work step-by-step:

Start with an empty list of seen colors.
Take the first ball and check if its color is in our list of seen colors.
If the color is not in the list, add it to the list.
Repeat the previous two steps for every ball in the collection.
Once we have processed all the balls, count how many colors are in the 'seen colors' list. This is the number of distinct colors.

Code Implementation

def find_distinct_colors_brute_force(balls):
    seen_colors = []

    for ball_color in balls:
        # Check if we've already encountered this color
        if ball_color not in seen_colors:

            # Only add the color if it's new
            seen_colors.append(ball_color)

    # Count the distinct colors now
    number_of_distinct_colors = len(seen_colors)
    return number_of_distinct_colors

Big(O) Analysis

Time Complexity

O(n²) – The algorithm iterates through each of the n balls in the collection. For each ball, it checks if its color is already present in the list of seen colors. In the worst case, the 'seen colors' list could grow to contain almost all n colors. Therefore, for each of the n balls, we may have to iterate through a list of up to n-1 already seen colors. This implies potentially n * (n-1) operations, which simplifies to O(n²).

Space Complexity

O(N) – The algorithm maintains a list of 'seen colors' to track distinct colors encountered. In the worst-case scenario, all N balls have a different color. This 'seen colors' list will grow linearly with the number of balls (N), storing each unique color. Thus, the auxiliary space required increases proportionally to N. Therefore, the space complexity is O(N).

Optimal Solution

Approach

The optimal way to solve this problem is to realize that we only need to count how many different colors exist. Using extra memory allows us to track seen colors efficiently. This avoids unnecessary comparisons or re-counting.

Here's how the algorithm would work step-by-step:

Start with an empty 'tracker' where we can remember the colors we've already seen.
Look at each ball one at a time.
For each ball, check if its color is already in our 'tracker'.
If the color is new (not in the 'tracker'), add it to the 'tracker'.
Continue looking at all the balls, adding any new colors to our 'tracker'.
Once we've looked at all the balls, count how many colors are in the 'tracker'. This is the number of distinct colors.
The final count is the answer to the question.

Code Implementation

def find_the_number_of_distinct_colors(
    balls_with_different_colors
):
    seen_colors = set()

    # We need to check each ball for unique colors
    for ball_color in balls_with_different_colors:
        # Only add to the set if we haven't seen it before
        if ball_color not in seen_colors:
            seen_colors.add(ball_color)

    # The length of the set is the number of distinct colors
    number_of_distinct_colors = len(seen_colors)

    return number_of_distinct_colors

Big(O) Analysis

Time Complexity

O(n) – The algorithm iterates through the input list of balls once. For each ball (n total balls), a check is performed to see if its color is already present in the 'tracker' (e.g., a set or hash table). Checking for existence in a set or hash table takes O(1) time on average. Therefore, the dominant operation is the single pass through the n balls, resulting in O(n) time complexity.

Space Complexity

O(N) – The algorithm uses a 'tracker' to store the distinct colors seen so far. In the worst-case scenario, where all N balls have different colors, the 'tracker' will need to store all N colors. Therefore, the auxiliary space required grows linearly with the number of balls, N. This results in a space complexity of O(N).

Edge Cases

Case	How to Handle
Null or Empty Input Array	Return 0, as there are no balls, and therefore no distinct colors.
Array with a Single Ball	Return 1, as there is only one ball, which represents a single distinct color.
Array with maximum possible integer values representing colors	The solution should efficiently handle large integer color values, potentially requiring a hash set or other suitable data structure for tracking seen colors.
Array with all balls having the same color	Return 1, as even though there are multiple balls, they are all the same color, so only one distinct color exists.
Array with a large number of distinct colors, approaching memory limits	Ensure that the chosen data structure for tracking distinct colors (e.g., HashSet) does not exceed available memory.
Input contains negative numbers representing colors	The solution should correctly interpret negative numbers as distinct color values and not treat them as errors or invalid input.
Very large array with many duplicate colors	Ensure the solution scales well by using a hash set or similar data structure which provides constant time average complexity for add and contains operations.
Integer Overflow if using sum of colors	Avoid using summing of colors for comparison/identification purposes; instead, rely on hash sets or similar distinct value identification techniques.

Null or Empty Input Array

How to Handle:

Return 0, as there are no balls, and therefore no distinct colors.

Array with a Single Ball

How to Handle:

Return 1, as there is only one ball, which represents a single distinct color.

Array with maximum possible integer values representing colors

How to Handle:

The solution should efficiently handle large integer color values, potentially requiring a hash set or other suitable data structure for tracking seen colors.

Array with all balls having the same color

How to Handle:

Return 1, as even though there are multiple balls, they are all the same color, so only one distinct color exists.

Array with a large number of distinct colors, approaching memory limits

How to Handle:

Ensure that the chosen data structure for tracking distinct colors (e.g., HashSet) does not exceed available memory.

Input contains negative numbers representing colors

How to Handle:

The solution should correctly interpret negative numbers as distinct color values and not treat them as errors or invalid input.

Very large array with many duplicate colors

How to Handle:

Ensure the solution scales well by using a hash set or similar data structure which provides constant time average complexity for add and contains operations.

Integer Overflow if using sum of colors

How to Handle:

Avoid using summing of colors for comparison/identification purposes; instead, rely on hash sets or similar distinct value identification techniques.