Find the Number of Ways to Place People I

Medium

Asked by:

8 views

Topics:

Arrays

You are given a 2D array points of size n x 2 representing integer coordinates of some points on a 2D plane, where points[i] = [x_i, y_i].

Count the number of pairs of points (A, B), where

A is on the upper left side of B, and
there are no other points in the rectangle (or line) they make (including the border).

Return the count.

Example 1:

Input: points = [[1,1],[2,2],[3,3]]

Output: 0

Explanation:

There is no way to choose A and B so A is on the upper left side of B.

Example 2:

Input: points = [[6,2],[4,4],[2,6]]

Output: 2

Explanation:

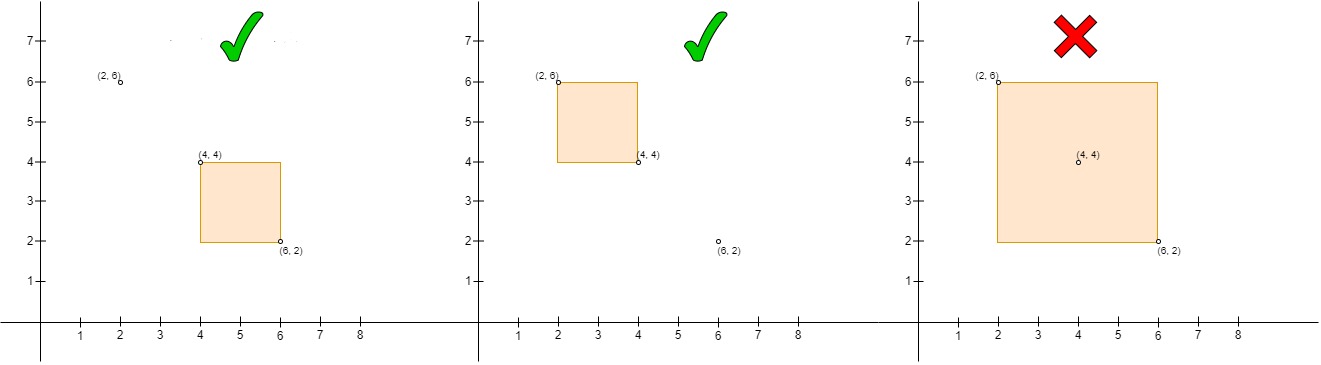
The left one is the pair (points[1], points[0]), where points[1] is on the upper left side of points[0] and the rectangle is empty.
The middle one is the pair (points[2], points[1]), same as the left one it is a valid pair.
The right one is the pair (points[2], points[0]), where points[2] is on the upper left side of points[0], but points[1] is inside the rectangle so it's not a valid pair.

Example 3:

Input: points = [[3,1],[1,3],[1,1]]

Output: 2

Explanation:

The left one is the pair (points[2], points[0]), where points[2] is on the upper left side of points[0] and there are no other points on the line they form. Note that it is a valid state when the two points form a line.
The middle one is the pair (points[1], points[2]), it is a valid pair same as the left one.
The right one is the pair (points[1], points[0]), it is not a valid pair as points[2] is on the border of the rectangle.

Constraints:

2 <= n <= 50
points[i].length == 2
0 <= points[i][0], points[i][1] <= 50
All points[i] are distinct.

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the dimensions of the room (number of rows and columns)?
Are the people identical or distinct? Does the order in which they are placed matter?
Are there any restrictions on where people can be placed (e.g., some cells are blocked)? If so, how will those be represented in the input?
What is the format of the input representing the room? Is it a 2D array, or something else?
Is there a maximum number of people that can be placed? If so, what is it?

Brute Force Solution

Approach

The brute force approach to this problem involves checking every single possible arrangement of people on the available seats. We try placing people in all possible seat combinations to see which ones satisfy the problem's condition. Because it checks everything, we are guaranteed to find the correct answer.

Here's how the algorithm would work step-by-step:

Start by considering the first person and placing them in the first available seat.
Then, try placing the first person in the second seat, the third seat, and so on, until you've tried all possible seats for the first person.
For each placement of the first person, consider the second person and try placing them in every remaining available seat.
Continue this process for each person, trying all possible seat assignments, one person at a time.
For each complete arrangement of people in seats, check if the arrangement meets any given conditions or constraints specified in the problem (e.g., people cannot sit next to each other).
Count the number of valid arrangements (arrangements that meet all the given conditions).
After trying all possible arrangements, report the total count of valid arrangements. This is your final answer.

Code Implementation

def find_the_number_of_ways_to_place_people_i(number_of_seats, number_of_people):
    number_of_valid_arrangements = 0

    def is_valid_arrangement(arrangement):
        return True

    def generate_arrangements(current_arrangement):
        nonlocal number_of_valid_arrangements

        if len(current_arrangement) == number_of_people:
            #An arrangement of people has been fully configured
            if is_valid_arrangement(current_arrangement):

                number_of_valid_arrangements += 1
            return

        #Iterate through each seat for placement of the next person
        for seat_index in range(number_of_seats):
            if seat_index not in current_arrangement:
                #Place the next person and continue to add more people

                generate_arrangements(current_arrangement + [seat_index])

    #Initiate the recursive arrangement builder with no one placed
    generate_arrangements([])

    return number_of_valid_arrangements

Big(O) Analysis

Time Complexity

O(n!) – The algorithm explores every possible arrangement of people in seats. If we have 'n' seats and 'k' people to place, the number of possible arrangements to examine is n * (n-1) * (n-2) * ... * (n-k+1). In the worst case, where we are placing 'n' people in 'n' seats (k=n), this becomes n * (n-1) * (n-2) * ... * 1, which is n factorial (n!). Thus, the time complexity is O(n!).

Space Complexity

O(N) – The brute force approach described utilizes recursion to explore all possible arrangements. The recursion depth corresponds to the number of people to be placed, which can be represented as N. At each level of recursion, we store the current arrangement of people in seats. Thus, the maximum depth of the recursion stack is N, and each level requires a constant amount of space for function call information. Therefore, the auxiliary space complexity is O(N).

Optimal Solution

Approach

The problem involves calculating the number of ways to arrange people in a row, considering constraints about who must sit together. The optimal approach is to treat each group that must sit together as a single unit and then calculate arrangements. Finally, account for arrangements within each group.

Here's how the algorithm would work step-by-step:

Identify the groups of people who must sit together.
Treat each group as a single entity or block.
Calculate the number of ways to arrange the blocks (groups) along with any individuals who don't have placement restrictions.
For each group, determine the number of ways to arrange the people within that group.
Multiply the number of arrangements of the blocks by the product of the number of internal arrangements for each group. This gives the final answer.

Code Implementation

def find_the_number_of_ways_to_place_people(number_of_people, groups):
    factorial_values = [1] * (number_of_people + 1)
    for i in range(2, number_of_people + 1):
        factorial_values[i] = factorial_values[i - 1] * i

    number_of_groups = len(groups)
    total_group_size = 0
    for group in groups:
        total_group_size += len(group)

    number_of_individual_people = number_of_people - total_group_size
    
    # Treat each group as one entity to determine arrangements
    number_of_entities = number_of_groups + number_of_individual_people
    number_of_ways_to_arrange_entities = factorial_values[number_of_entities]

    # Calculate arrangements within each group and apply to total
    group_arrangement_product = 1
    for group in groups:
        group_arrangement_product *= factorial_values[len(group)]

    # Multiply block arrangements by internal arrangements
    total_arrangements = number_of_ways_to_arrange_entities * group_arrangement_product

    return total_arrangements

Big(O) Analysis

Time Complexity

O(n!) – Identifying groups that must sit together can, in the worst case, involve iterating through all possible pairs or subsets, which isn't explicitly covered by the Big O estimate, but is vital to solution performance. Arranging the 'blocks' (groups and individuals) involves calculating the factorial of the number of blocks. Determining internal arrangements for each group also involves factorials, in the worst case. The final multiplication step contributes a negligible amount to the overall complexity. Because of the factorial computations for arranging blocks and elements within the blocks, the dominant term becomes O(n!), where n is the number of people.

Space Complexity

O(1) – The provided explanation focuses on calculating arrangements and does not describe the use of auxiliary data structures that scale with the input size. It mainly describes in-place manipulations and calculations. Therefore, the space complexity is constant, as no significant extra memory is allocated relative to the number of people, denoted as N. The calculations and grouping are assumed to be done without needing auxiliary arrays, lists, or hash maps that grow with N.

Edge Cases

Case	How to Handle
Empty input: n = 0 or fewer people	Return 1, as there is only one way to place no people (do nothing).
Small input: n = 1 person	Return 2, as there are two slots (left and right) for the single person.
Integer overflow for large n	Use a data type that can hold large numbers, such as long in Java/C++ or similar equivalents in other languages or explicitly handle overflow via modular arithmetic if the problem asks for the answer modulo a specific number.
Negative input (n < 0)	Throw an IllegalArgumentException or return 0, as the number of people cannot be negative, depending on the problem requirements.
Large value of n causing slow computation (performance bottleneck)	Optimize the solution using dynamic programming or memoization to avoid redundant calculations, reducing the time complexity to polynomial.
Constraints or dependencies on other people's placement (if the problem has added details)	Handle these by integrating them as additional validation within the placement algorithm or logic, verifying any criteria before confirming a position.
If specific positions are blocked or unavailable.	Represent the available positions using a boolean array or a set, and modify the algorithm to only consider valid positions.
If there are constraints on the distances between people	Add a distance check during placement to ensure the minimum distance requirement is met.

Empty input: n = 0 or fewer people

How to Handle:

Return 1, as there is only one way to place no people (do nothing).

Small input: n = 1 person

How to Handle:

Return 2, as there are two slots (left and right) for the single person.

Integer overflow for large n

How to Handle:

Use a data type that can hold large numbers, such as long in Java/C++ or similar equivalents in other languages or explicitly handle overflow via modular arithmetic if the problem asks for the answer modulo a specific number.

Negative input (n < 0)

How to Handle:

Throw an IllegalArgumentException or return 0, as the number of people cannot be negative, depending on the problem requirements.

Large value of n causing slow computation (performance bottleneck)

How to Handle:

Optimize the solution using dynamic programming or memoization to avoid redundant calculations, reducing the time complexity to polynomial.

Constraints or dependencies on other people's placement (if the problem has added details)

How to Handle:

Handle these by integrating them as additional validation within the placement algorithm or logic, verifying any criteria before confirming a position.

If specific positions are blocked or unavailable.

How to Handle:

Represent the available positions using a boolean array or a set, and modify the algorithm to only consider valid positions.

If there are constraints on the distances between people

How to Handle:

Add a distance check during placement to ensure the minimum distance requirement is met.