Longest Cycle in a Graph
HardYou are given a directed graph of n nodes numbered from 0 to n - 1, where each node has at most one outgoing edge.
The graph is represented with a given 0-indexed array edges of size n, indicating that there is a directed edge from node i to node edges[i]. If there is no outgoing edge from node i, then edges[i] == -1.
Return the length of the longest cycle in the graph. If no cycle exists, return -1.
A cycle is a path that starts and ends at the same node.
Example 1:
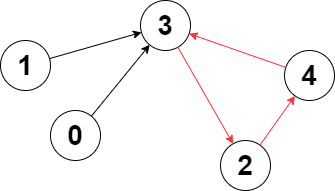
Input: edges = [3,3,4,2,3] Output: 3 Explanation: The longest cycle in the graph is the cycle: 2 -> 4 -> 3 -> 2. The length of this cycle is 3, so 3 is returned.
Example 2:
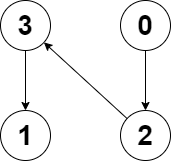
Input: edges = [2,-1,3,1] Output: -1 Explanation: There are no cycles in this graph.
Constraints:
n == edges.length2 <= n <= 105-1 <= edges[i] < nedges[i] != i
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What data type represents the graph, specifically how are the nodes and edges represented (e.g., adjacency list, adjacency matrix)?
- Is the graph directed or undirected?
- What should I return if there is no cycle in the graph? Should I return -1, null, or throw an exception?
- Can the graph be disconnected?
- Are there any constraints on the number of nodes or edges in the graph, such as a maximum number?
Brute Force Solution
Approach
The brute force way to find the longest cycle is to explore every possible path in the graph. We start from each node and try to find a path that leads back to the starting node, forming a cycle. By checking every single path, we can eventually determine the longest one.
Here's how the algorithm would work step-by-step:
- Pick a starting point in the graph.
- From that point, try every possible path by moving to a connected point, and then another, and another.
- As you explore each path, keep track of the points you've already visited.
- If you ever come back to the starting point, you've found a cycle.
- Calculate the length of that cycle (how many points are in it).
- Repeat this whole process starting from every other point in the graph.
- Compare the lengths of all the cycles you found.
- The longest one you found is the answer.
Code Implementation
def longest_cycle_brute_force(graph):
longest_cycle_length = 0
for start_node in range(len(graph)):
for path in find_all_cycles(graph, start_node):
cycle_length = len(path)
# Update the longest cycle length if necessary
if cycle_length > longest_cycle_length:
longest_cycle_length = cycle_length
return longest_cycle_length
def find_all_cycles(graph, start_node):
all_cycles = []
current_path = []
visited_nodes = set()
def dfs(current_node):
nonlocal all_cycles, current_path, visited_nodes
current_path.append(current_node)
visited_nodes.add(current_node)
# Explore neighbors
for neighbor_node in graph[current_node]:
if neighbor_node == start_node:
# Cycle is found, add it to the list
all_cycles.append(current_path[:] + [start_node])
elif neighbor_node not in visited_nodes:
dfs(neighbor_node)
# Backtrack
current_path.pop()
visited_nodes.remove(current_node)
# Initiate Depth First Search from starting node
dfs(start_node)
return all_cyclesBig(O) Analysis
Optimal Solution
Approach
The task is to find the longest loop in a directed graph. We can accomplish this efficiently by identifying starting points and then following each possible path to determine its length until we reach a loop or dead end.
Here's how the algorithm would work step-by-step:
- Identify all nodes in the graph that have no incoming connections. These will be our starting points for exploring paths.
- For each starting point, explore every possible path stemming from it using a method like depth-first search.
- As we explore a path, keep track of the nodes we've visited and the current path length.
- If we encounter a node we've already visited in the current path, this indicates a loop. Calculate the length of the loop.
- Keep track of the longest loop found so far. If we find a longer loop, update the longest loop length.
- If a path leads to a dead end (a node with no outgoing connections that doesn't form a cycle), stop exploring that path.
- After exploring all paths from all starting nodes, the longest loop found will be the answer.
Code Implementation
def longest_cycle(graph):
number_of_nodes = len(graph)
longest_cycle_length = -1
def depth_first_search(start_node):
nonlocal longest_cycle_length
visited = [False] * number_of_nodes
recursion_stack = [False] * number_of_nodes
path = []
def dfs_recursive(node):
nonlocal longest_cycle_length
visited[node] = True
recursion_stack[node] = True
path.append(node)
for neighbor in graph[node]:
if not visited[neighbor]:
dfs_recursive(neighbor)
elif recursion_stack[neighbor]:
# Cycle detected; calculate the cycle length.
cycle_start_index = path.index(neighbor)
cycle_length = len(path) - cycle_start_index
longest_cycle_length = max(longest_cycle_length, cycle_length)
recursion_stack[node] = False
path.pop()
dfs_recursive(start_node)
# Find nodes with no incoming edges to start DFS from.
indegrees = [0] * number_of_nodes
for node in range(number_of_nodes):
for neighbor in graph[node]:
indegrees[neighbor] += 1
starting_nodes = [node for node in range(number_of_nodes) if indegrees[node] == 0]
# If no nodes with in-degree zero, start from all nodes.
if not starting_nodes:
starting_nodes = list(range(number_of_nodes))
# Explore all possible paths from each starting node.
for start_node in starting_nodes:
depth_first_search(start_node)
# Crucial to run DFS from every node to find all cycles
for node in range(number_of_nodes):
if indegrees[node] > 0:
depth_first_search(node)
# Because DFS might not find every cycle.
visited_nodes = [False] * number_of_nodes
stack = []
def topological_sort(node):
visited_nodes[node] = True
for neighbor in graph[node]:
if not visited_nodes[neighbor]:
topological_sort(neighbor)
stack.append(node)
# Find all topological order for detecting cycles that DFS misses.
for node in range(number_of_nodes):
if not visited_nodes[node]:
topological_sort(node)
return longest_cycle_lengthBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty graph (no nodes) | Return 0 or an appropriate error value indicating no cycle exists. |
| Graph with only one node | Return 0, as a single node cannot form a cycle. |
| Graph with two nodes and one edge | Return 0, as two nodes with a single edge cannot form a cycle. |
| Graph with no cycles | Return 0, indicating that no cycle was found. |
| Graph with self-loops (edge from a node to itself) | Handle self-loops as a cycle of length 1, depending on problem constraints. |
| Disconnected graph (multiple components) | The algorithm should process each component independently to find the longest cycle among them. |
| Graph with very large number of nodes and edges (potential stack overflow with recursive DFS) | Use iterative DFS or BFS instead of recursive DFS to avoid stack overflow errors. |
| Graph with multiple cycles of the same maximum length | The algorithm should return any one of these longest cycles, unless specifically required to return all or a specific one. |