Maximal Network Rank

Medium

Asked by:

9 views

Topics:

Graphs

There is an infrastructure of n cities with some number of roads connecting these cities. Each roads[i] = [a_i, b_i] indicates that there is a bidirectional road between cities a_i and b_i.

The network rank of two different cities is defined as the total number of directly connected roads to either city. If a road is directly connected to both cities, it is only counted once.

The maximal network rank of the infrastructure is the maximum network rank of all pairs of different cities.

Given the integer n and the array roads, return the maximal network rank of the entire infrastructure.

Example 1:

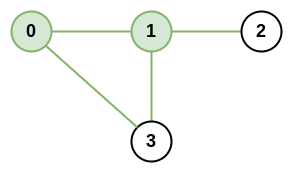
Input: n = 4, roads = [[0,1],[0,3],[1,2],[1,3]]
Output: 4
Explanation: The network rank of cities 0 and 1 is 4 as there are 4 roads that are connected to either 0 or 1. The road between 0 and 1 is only counted once.

Example 2:

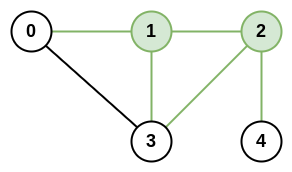
Input: n = 5, roads = [[0,1],[0,3],[1,2],[1,3],[2,3],[2,4]]
Output: 5
Explanation: There are 5 roads that are connected to cities 1 or 2.

Example 3:

Input: n = 8, roads = [[0,1],[1,2],[2,3],[2,4],[5,6],[5,7]]
Output: 5
Explanation: The network rank of 2 and 5 is 5. Notice that all the cities do not have to be connected.

Constraints:

2 <= n <= 100
0 <= roads.length <= n * (n - 1) / 2
roads[i].length == 2
0 <= a_i, b_i <= n-1
a_i != b_i
Each pair of cities has at most one road connecting them.

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What is the range for the number of nodes `n` and the number of roads in `roads`?
Can there be duplicate roads in the `roads` array, and if so, should they be treated as a single road or counted multiple times when determining the network rank?
Is it possible for a node to have a road connecting it to itself (a self-loop)? If so, how should that impact the degree calculation?
If the `roads` array is empty, meaning there are no roads connecting any cities, what should the function return?
Are the node IDs zero-based or one-based?

Brute Force Solution

Approach

The problem asks us to find the highest combined importance of any two cities, based on how many roads connect to them. The brute force strategy is to simply check every possible pair of cities and calculate their combined road connections.

Here's how the algorithm would work step-by-step:

Consider every possible pair of cities from the whole group of cities.
For each pair of cities, count the total number of roads connected to the first city and the total number of roads connected to the second city.
Add those two counts together to get a combined road count for that specific pair of cities.
If there is a road directly connecting the two cities we are currently looking at, subtract one from their combined road count because we don't want to double count that road.
Remember the highest combined road count we have seen so far.
After checking every possible pair of cities, the highest combined road count we have seen is the answer.

Code Implementation

def maximal_network_rank_brute_force(number_of_cities, roads):
    highest_network_rank = 0

    # Iterate through each possible pair of cities
    for first_city in range(number_of_cities):
        for second_city in range(first_city + 1, number_of_cities):
            first_city_connections = 0
            second_city_connections = 0

            # Count the roads connected to the first city
            for road in roads:
                if first_city in road:
                    first_city_connections += 1

            # Count the roads connected to the second city
            for road in roads:
                if second_city in road:
                    second_city_connections += 1

            current_network_rank = first_city_connections + second_city_connections

            # Subtract 1 if there's a road directly connecting the cities
            if [first_city, second_city] in roads or [second_city, first_city] in roads:
                current_network_rank -= 1

                # Ensure the highest rank is maintained

            if current_network_rank > highest_network_rank:
                highest_network_rank = current_network_rank

    return highest_network_rank

Big(O) Analysis

Time Complexity

O(n²) – The dominant operation in this approach is checking every possible pair of cities. With 'n' cities, we iterate through all possible pairs, which involves an outer loop effectively iterating 'n' times, and an inner loop also iterating approximately 'n' times to consider each city pair. Calculating the rank for each pair involves constant time operations. Thus the total number of operations is proportional to n * n, leading to a time complexity of O(n²).

Space Complexity

O(1) – The algorithm iterates through pairs of cities, calculating and comparing their combined road counts, but it does not create any auxiliary data structures that scale with the input size (number of cities or roads). Only a few integer variables are used to store intermediate counts and the maximum rank found so far. Therefore, the space complexity is constant, independent of the input size.

Optimal Solution

Approach

The goal is to find the pair of cities that, when combined, have the highest total number of roads connected to them. We need to consider the possibility that the two cities might be directly connected, which would cause us to double-count the connecting road, so we adjust for that.

Here's how the algorithm would work step-by-step:

First, count how many roads are connected to each individual city.
Then, consider every possible pair of cities.
For each pair, add the number of roads connected to each city in that pair to get a combined road count.
If the two cities in the pair are directly connected by a road, subtract one from the combined road count to correct for double-counting that road.
Keep track of the highest combined road count you find while going through all the pairs.
The highest combined road count you tracked is the final answer.

Code Implementation

def maximal_network_rank(number_of_nodes: int, roads: list[list[int]]) -> int:

    city_connections = [0] * number_of_nodes
    connected = [[False] * number_of_nodes for _ in range(number_of_nodes)]

    for road in roads:
        city_a, city_b = road
        city_connections[city_a] += 1
        city_connections[city_b] += 1
        connected[city_a][city_b] = True
        connected[city_b][city_a] = True

    max_network_rank = 0
    for city_a in range(number_of_nodes):
        for city_b in range(city_a + 1, number_of_nodes):
            # Sum roads connected to each city
            network_rank = city_connections[city_a] + city_connections[city_b]

            # Adjust for double counting if cities are connected
            if connected[city_a][city_b]:
                network_rank -= 1

            #Keep track of the highest combined road count
            max_network_rank = max(max_network_rank, network_rank)

    return max_network_rank

Big(O) Analysis

Time Complexity

O(n^2) – Calculating the degree of each city takes O(n) where n is the number of roads. The core of the algorithm involves iterating through all possible pairs of cities. With 'n' cities, there are approximately n * (n-1) / 2 possible pairs to consider. Checking if two cities are connected takes constant time O(1). Consequently, the dominant factor is the pairwise iteration, leading to a time complexity of O(n^2) because the n * (n-1) / 2 term simplifies to n^2 in Big O notation.

Space Complexity

O(N) – The space complexity is determined by the need to store the number of roads connected to each city. This requires an array (or similar data structure like a hash map) where the size is proportional to the number of cities, which we will denote as N. Therefore, auxiliary space is needed to store the degree (number of roads) for each of the N cities. Hence, the space complexity is O(N).

Edge Cases

Case	How to Handle
Empty roads array or n = 0	Return 0 since no network exists.
n = 1 (single city)	Return 0 as a single city cannot form a network.
All cities are connected to each other (complete graph)	The maximum degree of any node will be n-1, and the overlap calculation needs careful handling.
No roads exist (disconnected graph)	The degree of all nodes will be 0, so the maximum network rank will be 0.
Large n (number of cities) causing potential integer overflow when calculating degrees or network rank.	Use appropriate data types (e.g., long) to prevent integer overflow during calculations.
Duplicate entries in the roads array (same road listed multiple times)	The degree calculation should still be accurate as we are incrementing count, but consider de-duplicating the roads array to avoid unnecessary iterations if performance is critical.
Two cities have many roads connecting to the rest, skewing the rank	The algorithm will correctly find the two cities with the highest degree and adjust for their shared road, even with a skewed distribution.
Roads array contains invalid city indices (e.g., negative indices or indices >= n).	Validate input to ensure city indices are within the valid range [0, n-1] and throw an IllegalArgumentException if needed.

Empty roads array or n = 0

How to Handle:

Return 0 since no network exists.

n = 1 (single city)

How to Handle:

Return 0 as a single city cannot form a network.

All cities are connected to each other (complete graph)

How to Handle:

The maximum degree of any node will be n-1, and the overlap calculation needs careful handling.

No roads exist (disconnected graph)

How to Handle:

The degree of all nodes will be 0, so the maximum network rank will be 0.

Large n (number of cities) causing potential integer overflow when calculating degrees or network rank.

How to Handle:

Use appropriate data types (e.g., long) to prevent integer overflow during calculations.

Duplicate entries in the roads array (same road listed multiple times)

How to Handle:

The degree calculation should still be accurate as we are incrementing count, but consider de-duplicating the roads array to avoid unnecessary iterations if performance is critical.

Two cities have many roads connecting to the rest, skewing the rank

How to Handle:

The algorithm will correctly find the two cities with the highest degree and adjust for their shared road, even with a skewed distribution.

Roads array contains invalid city indices (e.g., negative indices or indices >= n).

How to Handle:

Validate input to ensure city indices are within the valid range [0, n-1] and throw an IllegalArgumentException if needed.