Maximum Matrix Sum
MediumYou are given an n x n integer matrix. You can do the following operation any number of times:
- Choose any two adjacent elements of
matrixand multiply each of them by-1.
Two elements are considered adjacent if and only if they share a border.
Your goal is to maximize the summation of the matrix's elements. Return the maximum sum of the matrix's elements using the operation mentioned above.
Example 1:
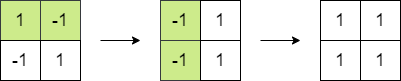
Input: matrix = [[1,-1],[-1,1]] Output: 4 Explanation: We can follow the following steps to reach sum equals 4: - Multiply the 2 elements in the first row by -1. - Multiply the 2 elements in the first column by -1.
Example 2:
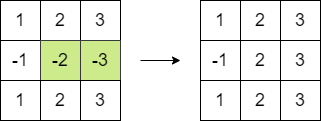
Input: matrix = [[1,2,3],[-1,-2,-3],[1,2,3]] Output: 16 Explanation: We can follow the following step to reach sum equals 16: - Multiply the 2 last elements in the second row by -1.
Constraints:
n == matrix.length == matrix[i].length2 <= n <= 250-105 <= matrix[i][j] <= 105
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the matrix, and what is the range of values that each element in the matrix can have? Can elements be negative, zero, or only positive?
- Can the input matrix be empty or null? What should I return in these cases?
- By 'maximum sum', do you mean the absolute maximum sum achievable by converting negative numbers to positive numbers according to the rules, or is there some other interpretation?
- If there are multiple ways to achieve the maximum sum, does it matter which combination of flips I use, or can I return any valid result?
- Can you provide a small example input and the expected output to illustrate the problem more clearly?
Brute Force Solution
Approach
To find the largest sum of a matrix by brute force, we essentially check every single possible combination of signs for each number in the matrix. We aim to maximize the sum by strategically flipping signs to eliminate negative numbers.
Here's how the algorithm would work step-by-step:
- Consider that each number in the matrix can either be positive or negative.
- Imagine going through every single possibility of positive or negative signs for each number in the matrix.
- For each of these possibilities, calculate the sum of all the numbers in the matrix.
- Keep track of the largest sum that you find from all of these calculations.
- After checking all possible combinations of positive and negative signs, the largest sum you've kept track of is your answer.
Code Implementation
def maximum_matrix_sum_brute_force(matrix):
number_of_rows = len(matrix)
number_of_columns = len(matrix[0])
total_elements = number_of_rows * number_of_columns
maximum_sum = float('-inf')
# Iterate through all possible sign combinations.
for i in range(2 ** total_elements):
current_sum = 0
temp_matrix = []
bitmask = bin(i)[2:].zfill(total_elements)
element_index = 0
for row in range(number_of_rows):
temp_row = []
for column in range(number_of_columns):
# Determine the sign based on the bitmask.
if bitmask[element_index] == '0':
temp_row.append(matrix[row][column])
current_sum += matrix[row][column]
else:
temp_row.append(-matrix[row][column])
current_sum += -matrix[row][column]
element_index += 1
temp_matrix.append(temp_row)
# Update maximum sum if current sum is larger.
if current_sum > maximum_sum:
maximum_sum = current_sum
return maximum_sumBig(O) Analysis
Optimal Solution
Approach
The goal is to maximize the sum of the matrix by cleverly manipulating negative numbers. The trick is to realize that pairs of negative numbers can be converted to positive numbers by flipping their signs strategically, and the number of negative numbers are important to the calculation.
Here's how the algorithm would work step-by-step:
- First, count how many negative numbers are in the matrix.
- Calculate the total sum of the absolute values of all the numbers in the matrix. This is like assuming all numbers are positive.
- If there are an even number of negative numbers, you can make them all positive with a series of sign flips. The maximum sum is simply the total absolute value sum calculated earlier.
- If there are an odd number of negative numbers, you can't get rid of all the negative signs. You'll be left with one negative number.
- To minimize the impact of the leftover negative number, find the smallest absolute value in the entire matrix.
- Subtract twice the smallest absolute value from the total absolute value sum. This is because you are essentially changing the sign of the smallest number from positive to negative, reducing the total by twice the number's value.
Code Implementation
def maximum_matrix_sum(matrix):
negative_number_count = 0
absolute_sum = 0
minimum_absolute_value = float('inf')
for row in matrix:
for number in row:
if number < 0:
negative_number_count += 1
absolute_value = abs(number)
absolute_sum += absolute_value
minimum_absolute_value = min(minimum_absolute_value, absolute_value)
# Even number of negatives can be flipped to positive.
if negative_number_count % 2 == 0:
return absolute_sum
# Odd number of negatives, one will remain negative.
# Minimize its impact by choosing smallest absolute value to negate.
# Subtract twice the minimum absolute value to account for sign change.
return absolute_sum - 2 * minimum_absolute_valueBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty matrix input | Return 0 immediately as there are no elements to sum. |
| Matrix with a single element | Return the absolute value of the single element. |
| Matrix with all positive numbers | Sum all elements directly as there is no benefit to flipping. |
| Matrix with all negative numbers | Flip all rows and columns to make all numbers positive, except for one if the matrix size is odd. |
| Matrix with a mix of positive, negative, and zero values | Count negative numbers, if even, sum absolute values; if odd, flip the smallest absolute value to negative. |
| Large matrix with integers near Integer.MAX_VALUE or Integer.MIN_VALUE, causing overflow during summation | Use long data type to store the intermediate and final sum to prevent integer overflow. |
| Matrix with many zeros | Zeros do not affect the sum and can be ignored when counting negative numbers and finding the smallest absolute value. |
| Matrix with dimensions close to maximum allowed array sizes | Ensure sufficient memory allocation and test with large inputs to prevent out-of-memory errors. |