Maximum Strictly Increasing Cells in a Matrix

Hard

Asked by:

12 views

Topics:

ArraysDynamic Programming

Given a 1-indexed m x n integer matrix mat, you can select any cell in the matrix as your starting cell.

From the starting cell, you can move to any other cell in the same row or column, but only if the value of the destination cell is strictly greater than the value of the current cell. You can repeat this process as many times as possible, moving from cell to cell until you can no longer make any moves.

Your task is to find the maximum number of cells that you can visit in the matrix by starting from some cell.

Return an integer denoting the maximum number of cells that can be visited.

Example 1:

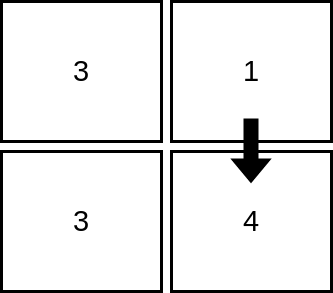
Input: mat = [[3,1],[3,4]]
Output: 2
Explanation: The image shows how we can visit 2 cells starting from row 1, column 2. It can be shown that we cannot visit more than 2 cells no matter where we start from, so the answer is 2.

Example 2:

Input: mat = [[1,1],[1,1]]
Output: 1
Explanation: Since the cells must be strictly increasing, we can only visit one cell in this example.

Example 3:

Input: mat = [[3,1,6],[-9,5,7]]
Output: 4
Explanation: The image above shows how we can visit 4 cells starting from row 2, column 1. It can be shown that we cannot visit more than 4 cells no matter where we start from, so the answer is 4.

Constraints:

m == mat.length
n == mat[i].length
1 <= m, n <= 10⁵
1 <= m * n <= 10⁵
-10⁵ <= mat[i][j] <= 10⁵

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the constraints on the dimensions of the matrix (number of rows and columns)?
What is the range of values for the integers within the matrix? Can they be negative, zero, or very large?
If the matrix is empty, or if there is no strictly increasing cell sequence, what should I return?
If there are multiple strictly increasing cell sequences with the same maximum length, can I return any one of them, or is there a specific one I should return based on some criteria (e.g., the one starting from the top-left corner)?
Can I move diagonally between cells, or am I restricted to moving only horizontally and vertically?

Brute Force Solution

Approach

The brute force method for this problem involves exploring all possible paths through the matrix. We want to find the longest possible path where each cell's value is strictly greater than the previous one. We accomplish this by starting from every cell and exploring all possible subsequent cells to build the longest path.

Here's how the algorithm would work step-by-step:

Begin by picking a cell in the matrix as the starting point of a potential path.
From that starting cell, consider every other cell in the same row or the same column.
Check if the value in the potential next cell is larger than the value in the current cell. If it is, we extend our path to include that cell.
Keep repeating the previous step: for the newest cell in our path, consider all other cells in its row or column and see if they are larger.
Whenever we reach a point where there are no more larger cells to move to in the same row or column, we have finished exploring one possible path.
Record the length of that path.
Now, do all of the previous steps again starting from a different cell in the matrix.
Continue this process, starting from every single cell in the matrix and exploring all possible paths from that cell.
After we have explored every possible path from every possible starting point, we compare the lengths of all the paths we recorded.
The longest path we found is the answer.

Code Implementation

def longest_increasing_path_brute_force(matrix):
    rows = len(matrix)
    columns = len(matrix[0])
    maximum_path_length = 0

    def find_longest_path(row_index, column_index, current_path_length):
        nonlocal maximum_path_length
        maximum_path_length = max(maximum_path_length, current_path_length)

        current_value = matrix[row_index][column_index]

        # Explore cells in the same row
        for next_column_index in range(columns):
            if next_column_index != column_index and \
               matrix[row_index][next_column_index] > current_value:

                find_longest_path(row_index, next_column_index, current_path_length + 1)

        # Explore cells in the same column
        for next_row_index in range(rows):
            if next_row_index != row_index and \
               matrix[next_row_index][column_index] > current_value:

                find_longest_path(next_row_index, column_index, current_path_length + 1)

    # Iterate through each cell to start a path.
    for row_index in range(rows):
        for column_index in range(columns):

            # Initiate the path from the current cell
            find_longest_path(row_index, column_index, 1)

    return maximum_path_length

Big(O) Analysis

Time Complexity

O(m * n * (m + n)!) – The algorithm starts at each cell in the m x n matrix, leading to m * n starting points. From each cell, it explores all possible paths by considering all other cells in the same row or column. In the worst case, from each cell, the number of possible paths can grow factorially because at each step we are choosing from roughly (m + n) cells to extend our path. Therefore, the time complexity is approximately O(m * n * (m + n)!).

Space Complexity

O(N) – The brute force algorithm explores all possible paths from each cell using recursion. In the worst-case scenario, the recursion depth could reach a maximum of N, where N is the total number of cells in the matrix (rows * cols), leading to N stack frames in the call stack. Therefore, the auxiliary space required for the recursion call stack can grow linearly with the number of cells in the matrix. Since the algorithm explores all possible paths, it must, at a minimum, implicitly keep track of the visited cells to avoid cycles in the explored paths, and the space for storing visited cells grows linearly with the total number of cells N.

Optimal Solution

Approach

The problem asks to find the longest path of increasing numbers by only moving right or down. We'll cleverly remember the longest path achievable at each value in the matrix as we encounter it, so we don't repeat calculations. This is achieved by processing the matrix in a specific order to ensure all necessary information is available when it's needed.

Here's how the algorithm would work step-by-step:

First, organize all the unique numbers found within the matrix in ascending order.
Start with the smallest number and process all occurrences of that number. The longest path from each occurrence of this smallest number will initially be just one (itself).
When processing each cell, look to the right and below. Find the maximum path length among all cells in the same row and column that we already know about. Add one to this maximum path length to obtain the length of the path from the current cell.
Store the maximum path length that can be achieved for each number.
Proceed to the next larger number and repeat the process, using and updating the stored path lengths for previously visited numbers.
Continue until all numbers are processed. The largest of all the stored path lengths is the result.

Code Implementation

def maximum_strictly_increasing_cells_in_a_matrix(matrix):
    rows = len(matrix)
    columns = len(matrix[0])

    unique_values = sorted(list(set(matrix[row][column] for row in range(rows) for column in range(columns))))

    longest_path = {}
    row_longest_path = [0] * rows
    column_longest_path = [0] * columns
    maximum_length = 0

    for value in unique_values:
        cells_with_current_value = []
        for row in range(rows):
            for column in range(columns):
                if matrix[row][column] == value:
                    cells_with_current_value.append((row, column))

        for row, column in cells_with_current_value:
            # Find max path from the same row or column
            max_path_length = max(row_longest_path[row], column_longest_path[column])
            longest_path[(row, column)] = max_path_length + 1
            maximum_length = max(maximum_length, longest_path[(row, column)])

        # Update longest path for row and column.
        for row, column in cells_with_current_value:
            row_longest_path[row] = max(row_longest_path[row], longest_path[(row, column)])
            column_longest_path[column] = max(column_longest_path[column], longest_path[(row, column)])

    return maximum_length

Big(O) Analysis

Time Complexity

O(m * n * log(m * n)) – Let m be the number of rows and n be the number of columns in the matrix. The algorithm first extracts and sorts all unique numbers in the matrix, which takes O(m * n * log(m * n)) time. After sorting, it iterates through each unique number. For each number, it iterates through all its occurrences in the matrix, which takes O(m * n) time in the worst case. Inside the inner loop, it finds the maximum path length in the corresponding row and column. Finding these maximums can be done in O(1) using precomputed row and column maximums, but the initial problem explanation doesn't mention that so we assume the worst case where we recompute for each cell, and that adds up to O(m + n) complexity. However given we only need to find a single max along the row and column, that doesn't impact the sort itself. Thus, the dominant factor remains the initial sorting step which yields a time complexity of O(m * n * log(m * n)).

Space Complexity

O(N) – The algorithm stores unique numbers from the matrix in ascending order, implying a list or set potentially holding all N elements of the matrix in the worst case (where all elements are distinct). It also maintains row and column path length information which requires two arrays (or dictionaries) of size M and K respectively, where M is the number of rows and K is the number of columns. In the worst case, where M and K are proportional to N, the space required for these arrays would also scale linearly with N. Therefore, the auxiliary space complexity is O(N).

Edge Cases

Case	How to Handle
Null or empty matrix	Return 0 immediately as no path can exist.
1x1 matrix	Return 1 as a single cell constitutes a path of length 1.
Matrix with all identical values	The longest path will be of length 1, as no strictly increasing sequence is possible.
Matrix with only negative numbers	The algorithm should correctly identify the longest strictly increasing path regardless of the sign of the numbers.
Matrix with duplicate values that could form multiple paths of same length	The algorithm should return the length of the longest path, regardless of how many exist.
Large matrix (e.g., 1000x1000) leading to potential stack overflow with recursion	Use dynamic programming with memoization to avoid excessive recursion depth and ensure scalability.
Integer overflow when calculating path lengths	Use a data type that can accommodate larger values, such as long, for storing path lengths.
Matrix with extremely large positive and negative numbers	The algorithm should handle extreme values correctly, ensuring the comparisons and updates work as expected without loss of precision or overflow, consider using appropriate data types.

Null or empty matrix

How to Handle:

Return 0 immediately as no path can exist.

1x1 matrix

How to Handle:

Return 1 as a single cell constitutes a path of length 1.

Matrix with all identical values

How to Handle:

The longest path will be of length 1, as no strictly increasing sequence is possible.

Matrix with only negative numbers

How to Handle:

The algorithm should correctly identify the longest strictly increasing path regardless of the sign of the numbers.

Matrix with duplicate values that could form multiple paths of same length

How to Handle:

The algorithm should return the length of the longest path, regardless of how many exist.

Large matrix (e.g., 1000x1000) leading to potential stack overflow with recursion

How to Handle:

Use dynamic programming with memoization to avoid excessive recursion depth and ensure scalability.

Integer overflow when calculating path lengths

How to Handle:

Use a data type that can accommodate larger values, such as long, for storing path lengths.

Matrix with extremely large positive and negative numbers

How to Handle:

The algorithm should handle extreme values correctly, ensuring the comparisons and updates work as expected without loss of precision or overflow, consider using appropriate data types.