Minimum Sideway Jumps

Medium

Asked by:

41 views

Topics:

ArraysDynamic Programming

There is a 3 lane road of length n that consists of n + 1 points labeled from 0 to n. A frog starts at point 0 in the second lane and wants to jump to point n. However, there could be obstacles along the way.

You are given an array obstacles of length n + 1 where each obstacles[i] (ranging from 0 to 3) describes an obstacle on the lane obstacles[i] at point i. If obstacles[i] == 0, there are no obstacles at point i. There will be at most one obstacle in the 3 lanes at each point.

For example, if obstacles[2] == 1, then there is an obstacle on lane 1 at point 2.

The frog can only travel from point i to point i + 1 on the same lane if there is not an obstacle on the lane at point i + 1. To avoid obstacles, the frog can also perform a side jump to jump to another lane (even if they are not adjacent) at the same point if there is no obstacle on the new lane.

For example, the frog can jump from lane 3 at point 3 to lane 1 at point 3.

Return the minimum number of side jumps the frog needs to reach any lane at point n starting from lane 2 at point 0.

Note: There will be no obstacles on points 0 and n.

Example 1:

Input: obstacles = [0,1,2,3,0]
Output: 2 
Explanation: The optimal solution is shown by the arrows above. There are 2 side jumps (red arrows).
Note that the frog can jump over obstacles only when making side jumps (as shown at point 2).

Example 2:

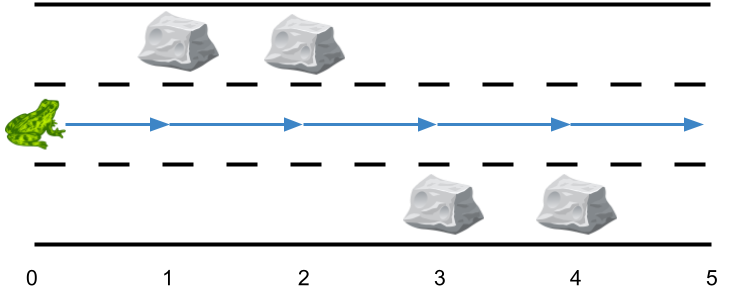
Input: obstacles = [0,1,1,3,3,0]
Output: 0
Explanation: There are no obstacles on lane 2. No side jumps are required.

Example 3:

Input: obstacles = [0,2,1,0,3,0]
Output: 2
Explanation: The optimal solution is shown by the arrows above. There are 2 side jumps.

Constraints:

obstacles.length == n + 1
1 <= n <= 5 * 10⁵
0 <= obstacles[i] <= 3
obstacles[0] == obstacles[n] == 0

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

The problem states 'lane i is represented by obstacles[i]'. However, the example implies `obstacles` is a 1D array representing positions and the lanes are implicit. Could you clarify if `obstacles` is a 2D array where `obstacles[lane][position]` or a 1D array where `obstacles[position]` indicates the obstacle type in each lane at that position?
The problem states 'The path from position 0 to the end is always possible.' Does this guarantee mean we don't need to handle cases where reaching the end is impossible, or should I still consider returning a specific value (e.g., -1) if, hypothetically, it were impossible?
Are the lane numbers 1, 2, and 3 inclusive? For example, can there be only 2 lanes or more than 3?
What is the expected output if the input `obstacles` array is empty or has only one position?
When jumping between lanes, can we jump from lane 1 to lane 3 or vice versa if lane 2 is clear at the current position? The problem statement says 'You cannot jump to lane 1 from lane 3 or vice versa,' but clarifies only adjacent lane jumps. Does this imply lane 1 and 3 are *never* considered adjacent for jumping purposes?

Brute Force Solution

Approach

Imagine you're navigating a path with obstacles. The brute force method involves exploring every single possible movement you could make, including all the times you might switch lanes to avoid a blockage. We'll consider every single sequence of choices.

Here's how the algorithm would work step-by-step:

Start at the beginning of the path.
For each position, consider all the possible lanes you can be in.
From your current position and lane, explore every valid next step forward.
If you encounter an obstacle in your current lane, consider all the sideways jumps to other lanes that allow you to continue forward.
For each of these potential jumps, count it as one 'sideways jump'.
Continue this process for every possible path you can take from the start to the end.
After exploring all possible paths, look at all the sequences of moves you made.
Find the path that required the absolute fewest sideways jumps.

Code Implementation

def minimum_sideway_jumps_brute_force(obstacles):
    numberOfLanes = len(obstacles[0])
    pathLength = len(obstacles)

    # Initialize a structure to store all possible paths and their jump counts.
    # This is crucial for exploring every combination.
    allPathsInformation = []

    def explore_paths(currentPosition, currentLane, currentSidewayJumps):
        if currentPosition == pathLength - 1:
            # Reached the end, record the path and its jumps.
            allPathsInformation.append(currentSidewayJumps)
            return

        # Check if the current lane has an obstacle at the next position.
        # If so, we must consider sideways jumps.
        if obstacles[currentPosition + 1][currentLane] == 1:
            for nextLane in range(numberOfLanes):
                if nextLane != currentLane and obstacles[currentPosition + 1][nextLane] == 0:
                    explore_paths(currentPosition + 1, nextLane, currentSidewayJumps + 1)
        else:
            # If no obstacle, we can move forward in the current lane.
            explore_paths(currentPosition + 1, currentLane, currentSidewayJumps)

    # Start exploration from each lane at the beginning of the path.
    for startingLane in range(numberOfLanes):
        if obstacles[0][startingLane] == 0:
            explore_paths(0, startingLane, 0)

    # Find the minimum number of sideway jumps across all explored paths.
    return min(allPathsInformation) if allPathsInformation else 0

Big(O) Analysis

Time Complexity

O(n) – The approach explores each position along the path, and at each position, it considers up to 3 lanes. The key operation is deciding the minimum jumps to reach the next position, which involves checking at most 3 other lanes. Since we do this for each of the n positions along the path, the total number of operations is roughly proportional to n multiplied by a small constant number of lane checks. This results in a linear time complexity of O(n).

Space Complexity

O(N) – The plain English explanation describes exploring every possible path. While not explicitly stated as a data structure, a recursive approach to explore all paths would implicitly use the call stack, which in the worst case can go as deep as N, representing the length of the path. Each recursive call would store local variables and return addresses. If a dynamic programming approach were used to store intermediate minimum jumps for each position and lane, it would require a 2D array of size 3xN, directly proportional to N. Therefore, the auxiliary space complexity is O(N).

Optimal Solution

Approach

Instead of checking every single path, we can figure out the cheapest way to reach each point by thinking about how we got there. We track the best cost to arrive at each spot on each lane, building up the solution step-by-step.

Here's how the algorithm would work step-by-step:

Imagine you are standing at the very beginning, before you even start moving.
For the first step forward, you can reach any of the three lanes. The cost to reach each lane at this first step is zero if you start there directly, or one if you have to make a sideway jump to get to it.
Now, for every subsequent step forward, consider your current position. You can either continue straight in your current lane, or you can jump to a different lane.
If you are at a particular spot and lane, figure out the cheapest way to get to this spot. This means considering the cost of arriving at the previous step in the same lane (no jump), or the cost of arriving at the previous step in a different lane and then jumping over.
Keep track of the minimum cost to reach each spot on each of the three lanes.
If there's a barrier at a certain spot in a particular lane, you cannot enter that lane at that spot. So, the cost to reach that spot in that lane is effectively infinite.
After you have processed all the steps forward, look at the very last spot. The minimum cost to reach the end is the smallest of the costs to reach the final spot on any of the three lanes.
By always choosing the cheapest option at each step, you guarantee that you find the overall minimum number of sideway jumps needed.

Code Implementation

def min_sideway_jumps(obstacles):
    numberOfPoints = len(obstacles)
    # Initialize costs for reaching each point on each lane.
    # Costs represent minimum sideway jumps to reach that point.
    # We initialize with a large number to simulate infinity for unreachable points.
    costsToReachPoint = [[float('inf')] * 3 for _ in range(numberOfPoints + 1)]

    # Base case: At the start (before point 0), cost to be on any lane is 0.
    # If there's no obstacle at point 0, we can be on that lane with 0 jumps.
    for laneIndex in range(3):
        if obstacles[0] != laneIndex + 1:
            costsToReachPoint[0][laneIndex] = 0

    # Iterate through each point from the start to the end.
    for currentPointIndex in range(numberOfPoints):
        # For each lane, determine the minimum cost to reach the next point.
        for currentLaneIndex in range(3):
            # If the current point on the current lane is blocked, skip it.
            if obstacles[currentPointIndex] == currentLaneIndex + 1:
                continue

            # Option 1: Move straight to the next point in the same lane.
            # The cost is the same as reaching the current point in this lane.
            costStraight = costsToReachPoint[currentPointIndex][currentLaneIndex]

            # Option 2: Jump to a different lane at the next point.
            # This involves the cost of reaching the current point in a different lane
            # plus one jump, or reaching the current point in the same lane and jumping.
            # We find the minimum cost to reach the current point across all lanes.
            minimumCostAtCurrentPoint = float('inf')
            for previousLaneIndex in range(3):
                minimumCostAtCurrentPoint = min(minimumCostAtCurrentPoint, costsToReachPoint[currentPointIndex][previousLaneIndex])

            # Cost of jumping from another lane to the current lane at the next point.
            # This is the minimum cost to reach currentPointIndex on ANY lane + 1 (for the jump).
            # This considers all possibilities to arrive at currentPointIndex.
            costSideway = minimumCostAtCurrentPoint + 1

            # Update the cost to reach the next point in the current lane.
            # We take the minimum of staying in the same lane (if possible) or jumping.
            nextPointIndex = currentPointIndex + 1
            if nextPointIndex < numberOfPoints + 1:
                # If we can move straight, consider that cost.
                if obstacles[nextPointIndex] != currentLaneIndex + 1:
                    costsToReachPoint[nextPointIndex][currentLaneIndex] = min(
                        costsToReachPoint[nextPointIndex][currentLaneIndex], 
                        costStraight
                    )
                # Also consider the cost from jumping from ANY lane at currentPointIndex
                # to currentLaneIndex at nextPointIndex.
                # This represents the possibility of jumping to currentLaneIndex at nextPointIndex.
                if obstacles[nextPointIndex] != currentLaneIndex + 1:
                    costsToReachPoint[nextPointIndex][currentLaneIndex] = min(
                        costsToReachPoint[nextPointIndex][currentLaneIndex], 
                        costSideway
                    )

    # The final answer is the minimum cost to reach the last point on any of the three lanes.
    return min(costsToReachPoint[numberOfPoints])

Big(O) Analysis

Time Complexity

O(n) – The algorithm iterates through each of the n points (or steps) along the path. For each point, it considers the three possible lanes. Within each point and lane consideration, it performs a constant number of operations to calculate the minimum cost to reach that state, involving checking the costs from the previous step in potentially all three lanes. Since these constant-time operations are performed for each of the n points, the total time complexity is directly proportional to n, resulting in O(n).

Space Complexity

O(1) – The solution primarily uses a few variables to keep track of the minimum cost to reach each of the three lanes at the current step. These variables store constant amounts of information regardless of the input size N (number of obstacles). Therefore, the auxiliary space complexity is constant.

Edge Cases

Case	How to Handle
Input array 'obstacles' is null or empty	The problem statement guarantees a valid path is always possible, implying the input array will not be null or empty and will have at least one position.
Array with only one position	If the array has only one position, no jumps are needed, and the initial lane 2 is valid, resulting in 0 sideway jumps.
All positions have obstacles in all three lanes	The problem statement guarantees a path is always possible, meaning this scenario where no movement or jumps are allowed will not occur.
Obstacles are only present in lanes 1 and 3, not lane 2	This scenario is valid and the algorithm should simply move forward in lane 2 without any sideway jumps.
Obstacles are present in lane 2 at the starting position (position 0)	The problem states the initial position is in lane 2, and the first position cannot have an obstacle if we are to start there. If it did, it would imply an impossible starting state according to the rules.
The path requires constant sideway jumps	A dynamic programming approach or breadth-first search can efficiently track the minimum jumps to reach each position in each lane, handling such scenarios.
The array is extremely large	A dynamic programming solution with O(N) time complexity and O(N) space complexity (or O(1) if optimized) will scale efficiently for large inputs.
The destination lane for a sideway jump is blocked at the current position	The algorithm must explicitly check for obstacles in the destination lane before making a sideway jump, as per the problem rules.

Input array 'obstacles' is null or empty

How to Handle:

The problem statement guarantees a valid path is always possible, implying the input array will not be null or empty and will have at least one position.

Array with only one position

How to Handle:

If the array has only one position, no jumps are needed, and the initial lane 2 is valid, resulting in 0 sideway jumps.

All positions have obstacles in all three lanes

How to Handle:

The problem statement guarantees a path is always possible, meaning this scenario where no movement or jumps are allowed will not occur.

Obstacles are only present in lanes 1 and 3, not lane 2

How to Handle:

This scenario is valid and the algorithm should simply move forward in lane 2 without any sideway jumps.

Obstacles are present in lane 2 at the starting position (position 0)

How to Handle:

The problem states the initial position is in lane 2, and the first position cannot have an obstacle if we are to start there. If it did, it would imply an impossible starting state according to the rules.

The path requires constant sideway jumps

How to Handle:

A dynamic programming approach or breadth-first search can efficiently track the minimum jumps to reach each position in each lane, handling such scenarios.

The array is extremely large

How to Handle:

A dynamic programming solution with O(N) time complexity and O(N) space complexity (or O(1) if optimized) will scale efficiently for large inputs.

The destination lane for a sideway jump is blocked at the current position

How to Handle:

The algorithm must explicitly check for obstacles in the destination lane before making a sideway jump, as per the problem rules.