Number of Good Leaf Nodes Pairs
MediumYou are given the root of a binary tree and an integer distance. A pair of two different leaf nodes of a binary tree is said to be good if the length of the shortest path between them is less than or equal to distance.
Return the number of good leaf node pairs in the tree.
Example 1:
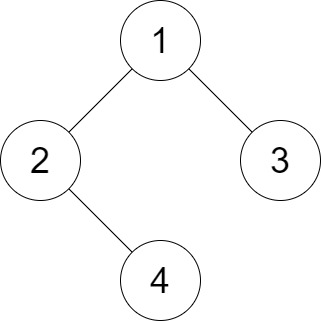
Input: root = [1,2,3,null,4], distance = 3 Output: 1 Explanation: The leaf nodes of the tree are 3 and 4 and the length of the shortest path between them is 3. This is the only good pair.
Example 2:
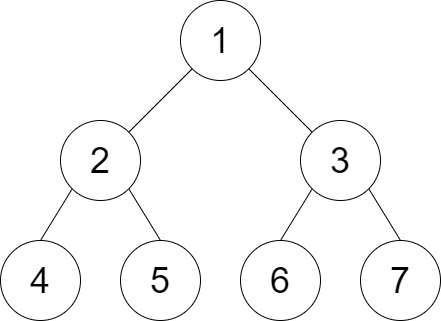
Input: root = [1,2,3,4,5,6,7], distance = 3 Output: 2 Explanation: The good pairs are [4,5] and [6,7] with shortest path = 2. The pair [4,6] is not good because the length of ther shortest path between them is 4.
Example 3:
Input: root = [7,1,4,6,null,5,3,null,null,null,null,null,2], distance = 3 Output: 1 Explanation: The only good pair is [2,5].
Constraints:
- The number of nodes in the
treeis in the range[1, 210]. 1 <= Node.val <= 1001 <= distance <= 10
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for the node values in the tree, and what is the maximum height or number of nodes in the tree?
- Can the value of 'distance' be zero or negative?
- What constitutes a 'good leaf node pair'? Is it that the distance between them is *less than or equal to* the given distance, or strictly *less than*?
- If no good leaf node pairs exist within the given distance, what should the function return? (e.g., 0, -1, null)?
- Is the input always a valid binary tree, or do I need to handle cases where the tree might be null or empty?
Brute Force Solution
Approach
The brute force approach to counting good leaf node pairs in a tree involves examining every possible pairing of leaf nodes. For each pair, we'll determine if they're a 'good' pair based on a distance constraint. Finally, we count the total number of good pairs found by exploring all possibilities.
Here's how the algorithm would work step-by-step:
- First, identify all the leaf nodes in the tree (nodes without any children).
- Then, take the first leaf node and pair it with every other leaf node in the tree, including itself.
- For each of these pairs, calculate the distance between the two leaf nodes in the tree. The distance is the number of connections you need to travel along to get from one node to the other.
- If the distance between the pair is less than or equal to the given distance threshold, mark this pair as 'good'.
- Repeat this process, pairing the second leaf node with every other leaf node, calculating distances, and marking good pairs.
- Continue this process for every leaf node in the tree, making sure to pair it with all other leaf nodes.
- Finally, count the total number of 'good' pairs you found throughout the entire process. This is the number of good leaf node pairs.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def count_good_leaf_node_pairs_brute_force(root, distance_threshold):
def get_all_leaf_nodes(node, leaf_nodes_list):
if not node:
return
if not node.left and not node.right:
leaf_nodes_list.append(node)
return
get_all_leaf_nodes(node.left, leaf_nodes_list)
get_all_leaf_nodes(node.right, leaf_nodes_list)
def calculate_distance(node1, node2):
#Find the distance between two nodes
def find_path(root, target, path):
if not root:
return False
path.append(root)
if root == target:
return True
if find_path(root.left, target, path) or find_path(root.right, target, path):
return True
path.pop()
return False
path_node1 = []
path_node2 = []
find_path(root, node1, path_node1)
find_path(root, node2, path_node2)
# Find the common ancestor.
common_ancestor_index = 0
while common_ancestor_index < min(len(path_node1), len(path_node2)) and \
path_node1[common_ancestor_index] == path_node2[common_ancestor_index]:
common_ancestor_index += 1
# Calculate the distance.
distance = len(path_node1) + len(path_node2) - 2 * common_ancestor_index
return distance
leaf_nodes = []
get_all_leaf_nodes(root, leaf_nodes)
good_leaf_node_pairs_count = 0
#Iterate through all the leaves
for first_leaf_node_index in range(len(leaf_nodes)):
for second_leaf_node_index in range(len(leaf_nodes)):
#Calculate the distance between each pair of leaves
distance = calculate_distance(leaf_nodes[first_leaf_node_index], leaf_nodes[second_leaf_node_index])
#Check if the pair is good based on distance
if distance <= distance_threshold:
good_leaf_node_pairs_count += 1
return good_leaf_node_pairs_countBig(O) Analysis
Optimal Solution
Approach
The best way to solve this is to explore the tree systematically, keeping track of the distance to the leaf nodes. At each node, we combine the information from its children to count the number of 'good' pairs efficiently.
Here's how the algorithm would work step-by-step:
- Imagine exploring the tree starting from the very top, going deeper and deeper.
- Whenever you reach a leaf node, record that you've found it and its distance from the top where you started.
- As you go back up the tree, when you are at a parent node, get the information from its left and right children.
- For every leaf found on the left side, and every leaf found on the right side, check if the sum of their distances is less than or equal to the given limit.
- If the sum of their distances is within the limit, count this pair as a 'good' pair.
- Now, pass all the leaves and their distances found back up to the next parent node.
- Continue doing this until you reach the very top of the tree. The total number of 'good' pairs you counted is your final answer.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def countPairs(self, root: TreeNode, distance: int) -> int:
self.good_node_pairs_count = 0
def dfs(node: TreeNode) -> list[int]:
if not node:
return []
if not node.left and not node.right:
return [0]
left_leaf_distances = dfs(node.left)
right_leaf_distances = dfs(node.right)
# Count good pairs between left and right subtrees
for left_distance in left_leaf_distances:
for right_distance in right_leaf_distances:
if left_distance + right_distance + 2 <= distance:
self.good_node_pairs_count += 1
# Propagate distances to the parent node
updated_distances = []
for distance_val in left_leaf_distances:
if distance_val + 1 < distance:
updated_distances.append(distance_val + 1)
for distance_val in right_leaf_distances:
if distance_val + 1 < distance:
updated_distances.append(distance_val + 1)
return updated_distances
dfs(root)
return self.good_node_pairs_countBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty tree root | Return 0 if the root is null or the tree is empty as there are no leaf nodes. |
| Tree with only one node (root is also a leaf) | Return 0 as there are no pairs of leaf nodes. |
| Tree where all leaves are at distance greater than distance | Return 0, indicating no good leaf node pairs are found within the specified distance. |
| Tree where all leaves are at distance less than or equal to distance | The solution should correctly count all possible leaf node pairs. |
| Skewed tree (e.g., all nodes on one side) | The recursion should handle the deep call stack without causing a stack overflow error, and the distance calculations remain valid. |
| Large tree with a large 'distance' value | Ensure the algorithm's time complexity is efficient enough to handle the large input size and distance, avoiding performance bottlenecks. |
| Tree with many leaves clustered close to each other | The algorithm must avoid double-counting pairs of leaf nodes. |
| Negative or zero distance provided as input | Treat negative or zero distance values as invalid input and return 0 or throw an IllegalArgumentException. |