Partition List
MediumGiven the head of a linked list and a value x, partition it such that all nodes less than x come before nodes greater than or equal to x.
You should preserve the original relative order of the nodes in each of the two partitions.
Example 1:
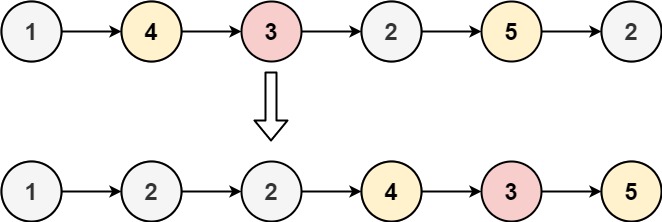
Input: head = [1,4,3,2,5,2], x = 3 Output: [1,2,2,4,3,5]
Example 2:
Input: head = [2,1], x = 2 Output: [1,2]
Constraints:
- The number of nodes in the list is in the range
[0, 200]. -100 <= Node.val <= 100-200 <= x <= 200
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the data type of the list elements and the partition value 'x'? Are they integers, floats, or something else?
- Can the input list be empty or null? What should I return in those cases?
- If a node's value is equal to 'x', where should it be placed in the partitioned list: before or after the group of nodes less than 'x'?
- Does the relative order of nodes within each partition (less than x and greater than or equal to x) need to be preserved?
- Is it guaranteed that 'x' will be present in the list? If not, how should I handle that scenario?
Brute Force Solution
Approach
The goal is to rearrange a linked list so that all values less than a given number come before all values greater than or equal to it. A brute force method involves creating two separate temporary storage areas. We then place the elements accordingly and combine them.
Here's how the algorithm would work step-by-step:
- Create one storage area to temporarily hold all values from the original list that are less than the given number.
- Create another separate storage area to hold all the other values (those greater than or equal to the given number).
- Go through the original list, one value at a time.
- If a value is less than the given number, put it into the first storage area.
- Otherwise, put the value into the second storage area.
- Once we've moved all the values from the original list, take all the values from the first storage area and put them back into a new linked list.
- Then, take all the values from the second storage area and add them to the end of that new linked list.
- The resulting linked list is the rearranged list.
Code Implementation
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
def partition_list_brute_force(head, partition_value):
less_than_partition = []
greater_equal_partition = []
current_node = head
while current_node:
# Append values to respective lists based on comparison.
if current_node.val < partition_value:
less_than_partition.append(current_node.val)
else:
greater_equal_partition.append(current_node.val)
current_node = current_node.next
new_head = None
tail = None
# Rebuild linked list using values from less_than_partition.
for value in less_than_partition:
new_node = ListNode(value)
if not new_head:
new_head = new_node
tail = new_node
else:
tail.next = new_node
tail = new_node
# Append values from greater_equal_partition.
for value in greater_equal_partition:
new_node = ListNode(value)
if not new_head:
new_head = new_node
tail = new_node
else:
# Only set if there are values in the first list.
if tail:
tail.next = new_node
else:
new_head = new_node
tail = new_node
return new_headBig(O) Analysis
Optimal Solution
Approach
The goal is to rearrange a linked list so that all the smaller values come before a specific value, and all the larger values come after it, keeping the original order within each group. We do this by creating two separate lists, one for smaller values and one for larger values, and then joining them together.
Here's how the algorithm would work step-by-step:
- Imagine you have two empty boxes, one for numbers smaller than the target and another for numbers larger than the target.
- Go through each number in the original list, one at a time.
- If a number is smaller than the target, put it in the 'smaller' box.
- If a number is larger than the target, put it in the 'larger' box.
- Once you've processed all the numbers, take the 'smaller' box and connect it to the front of the 'larger' box. This combines the two lists in the desired order.
Code Implementation
def partition_list(head, partition_value):
smaller_head = None
smaller_tail = None
larger_head = None
larger_tail = None
current_node = head
while current_node:
next_node = current_node.next
if current_node.val < partition_value:
# Build the list of nodes smaller than the partition value.
if smaller_head is None:
smaller_head = current_node
smaller_tail = current_node
else:
smaller_tail.next = current_node
smaller_tail = current_node
else:
# Build the list of nodes larger than or equal to the partition value.
if larger_head is None:
larger_head = current_node
larger_tail = current_node
else:
larger_tail.next = current_node
larger_tail = current_node
current_node = next_node
if larger_tail is not None:
larger_tail.next = None
# If there are no smaller nodes, return the larger list.
if smaller_head is None:
return larger_head
# Connect the smaller list to the larger list.
smaller_tail.next = larger_head
# Return the head of the combined list.
return smaller_headBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty list or null input list | Return the original list or null, as there's nothing to partition. |
| List with only one element | Return the original list, as it's already 'partitioned'. |
| Partition value is smaller than all elements in the list | All elements should be moved to the 'greater than or equal' partition (right partition), leaving the 'less than' partition empty. |
| Partition value is larger than all elements in the list | All elements should be moved to the 'less than' partition (left partition), leaving the 'greater than or equal' partition empty. |
| List contains duplicate values, some smaller and some greater than the partition value | The duplicates should be grouped correctly on either side of the partition according to their value relative to the partition. |
| List is already partitioned correctly according to the value | The solution should not modify the list in any way and should return it directly. |
| List contains negative numbers, zeros, and positive numbers | The solution should correctly handle all types of numbers and partition them based on their relation to the partition value. |
| Integer overflow if comparing very large numbers in the linked list | The solution should use appropriate comparison operators (e.g., using long type or other mitigation techniques depending on language/environment) to prevent integer overflow. |