Path In Zigzag Labelled Binary Tree
MediumIn an infinite binary tree where every node has two children, the nodes are labelled in row order.
In the odd numbered rows (ie., the first, third, fifth,...), the labelling is left to right, while in the even numbered rows (second, fourth, sixth,...), the labelling is right to left.
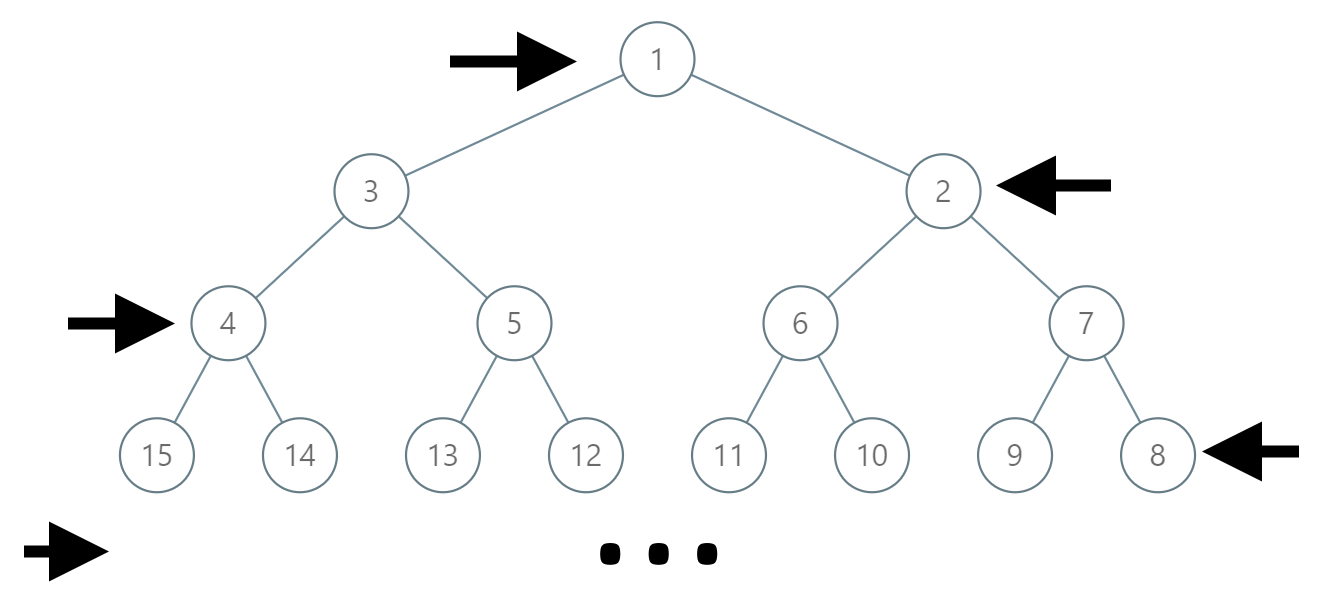
Given the label of a node in this tree, return the labels in the path from the root of the tree to the node with that label.
Example 1:
Input: label = 14 Output: [1,3,4,14]
Example 2:
Input: label = 26 Output: [1,2,6,10,26]
Constraints:
1 <= label <= 10^6
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- For determining the zig-zag labeling pattern, is the root of the tree considered to be at row 1 or row 0?
- The output in the examples is a list of labels from the root to the target node. Is this specific ordering required for the result?
- Can I assume the root of the tree is always labeled with the value 1?
- Since the tree is described as 'infinite', is the expectation that I find the path by mathematically computing the parent of a node from its label, rather than building the tree in memory?
- Given the constraints and the labeling scheme, should I assume that any `label` provided as input is guaranteed to exist within the tree?
Brute Force Solution
Approach
The brute force approach is to actually construct a model of this special zigzag tree, level by level, until we reach the given number. Once the number is placed in our model tree, we can simply trace its connections backward to find the path to the top.
Here's how the algorithm would work step-by-step:
- First, start by creating a representation of the tree, beginning with the top node, which is always the number 1.
- Then, generate the next level of the tree. Figure out the range of numbers for this level and decide whether they should be placed from left-to-right or right-to-left, according to the zigzag pattern.
- While adding each number to the new level, make sure to connect it to its parent from the level above.
- Repeat this process of adding new levels, alternating the placement direction each time, until you have built the tree down to the level that contains your target number.
- Once the tree is built far enough, find the location of your target number within it.
- Starting from your target number, work your way back up the tree by repeatedly moving to the parent node, keeping track of every number you visit on this upward journey.
- Finally, since the path is from the top down, you just need to reverse the sequence of numbers you collected to get the final answer.
Code Implementation
def pathInZigZagTree_brute_force(target_label):
if target_label == 1:
return [1]
# This map stores parent-child links, which are essential for tracing the path back to the root.
parent_of_node_map = {}
nodes_at_parent_level = [1]
current_tree_level = 0
while True:
current_tree_level += 1
level_start_label = 2 ** current_tree_level
level_end_label = 2 ** (current_tree_level + 1) - 1
# Labels are generated in either normal or reverse order to match the zigzag pattern of the tree.
is_level_left_to_right = current_tree_level % 2 == 0
labels_for_new_level = []
if is_level_left_to_right:
labels_for_new_level = list(range(level_start_label, level_end_label + 1))
else:
labels_for_new_level = list(range(level_end_label, level_start_label - 1, -1))
nodes_at_child_level = []
is_target_in_this_level = False
for parent_list_index in range(len(nodes_at_parent_level)):
parent_node_value = nodes_at_parent_level[parent_list_index]
child_one_value = labels_for_new_level[parent_list_index * 2]
child_two_value = labels_for_new_level[parent_list_index * 2 + 1]
parent_of_node_map[child_one_value] = parent_node_value
parent_of_node_map[child_two_value] = parent_node_value
nodes_at_child_level.append(child_one_value)
nodes_at_child_level.append(child_two_value)
if child_one_value == target_label or child_two_value == target_label:
is_target_in_this_level = True
nodes_at_parent_level = nodes_at_child_level
# We can stop building the tree once the level containing our target label has been constructed.
if is_target_in_this_level:
break
path_from_target_to_root = []
current_node_in_path = target_label
while current_node_in_path in parent_of_node_map:
path_from_target_to_root.append(current_node_in_path)
current_node_in_path = parent_of_node_map[current_node_in_path]
path_from_target_to_root.append(1)
# The path was built from target-to-root, so we reverse it to get the required root-to-target order.
path_from_root_to_target = path_from_target_to_root[::-1]
return path_from_root_to_targetBig(O) Analysis
Optimal Solution
Approach
The most efficient way to solve this is to work backward from the given number up to the root of the tree. The core insight is that we can treat the tree as a normal binary tree if we first convert each number from its zigzag position to its 'regular' position. This mathematical trick lets us find any node's parent easily without ever needing to build the tree.
Here's how the algorithm would work step-by-step:
- Start with the final number (the label) and make it the beginning of our result path.
- As long as we haven't reached the root of the tree (which is always the number 1), we will repeatedly find the parent of the last number we found.
- To find a number's parent, first figure out which level of the tree it lives on based on its value.
- Every level has a specific range of numbers, from a smallest possible value to a largest. Find this range for the current number's level.
- Now for the key trick: find the number's 'mirror image' value on its level. This tells you what the number would be if its row wasn't labelled backwards. You find this by adding the smallest and largest values of the level's range and then subtracting your current number.
- Once you have this 'regular' number, finding its parent is simple: just divide that number by two.
- This result is the true parent we're looking for. Add it to the front of our result path, and then repeat the process for this new parent number.
- When we finally reach the number 1, our path from the root to the target is complete and in the correct order.
Code Implementation
def pathInZigZagTree(label: int) -> list[int]:
path_result = []
current_node_label = label
while current_node_label >= 1:
path_result.insert(0, current_node_label)
if current_node_label == 1:
break
# The level index is crucial as it determines if labels are ordered normally or in reverse.
current_level = current_node_label.bit_length() - 1
true_value_for_parent_calc = current_node_label
# On reversed levels, we find the node's symmetrical value to map it back to a standard tree.
if current_level % 2 != 0:
level_start_value = 1 << current_level
level_end_value = (1 << (current_level + 1)) - 1
true_value_for_parent_calc = (level_start_value + level_end_value) - current_node_label
# Once normalized to a standard tree position, the parent is found by integer division.
parent_label = true_value_for_parent_calc // 2
current_node_label = parent_label
return path_resultBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Input label is the root of the tree (label = 1). | The algorithm should handle this base case by correctly returning a path containing only the root, `[1]`. |
| Label is on the second row (e.g., 2 or 3), the first right-to-left ordered level. | This tests the core zigzag logic on the shallowest possible level where the ordering is reversed. |
| Label is the first node of a left-to-right level (e.g., label = 4). | The parent calculation must correctly handle a zero positional offset when the node is at the start of its level's range. |
| Label is the last node of a right-to-left level (e.g., label = 8). | The solution must correctly find the parent when the node is at the end of a reversed level, which corresponds to the start position conceptually. |
| Maximum input label near 10^6. | The solution's intermediate calculations for level boundaries must not cause an integer overflow, even for the deepest levels required by the constraints. |
| The algorithm naturally constructs the path backwards. | The final list of nodes must be reversed before returning to show the correct root-to-label path. |
| A label whose parent is in a level with the opposite ordering. | The algorithm must translate the parent's conceptual position into its actual label based on the parent level's specific ordering convention. |
| Determining a node's level from its label. | Using integer-based methods like bit shifts is more robust for finding the level than using floating-point `log2` which can have precision errors. |