Print Binary Tree
MediumGiven the root of a binary tree, construct a 0-indexed m x n string matrix res that represents a formatted layout of the tree. The formatted layout matrix should be constructed using the following rules:
- The height of the tree is
heightand the number of rowsmshould be equal toheight + 1. - The number of columns
nshould be equal to2height+1 - 1. - Place the root node in the middle of the top row (more formally, at location
res[0][(n-1)/2]). - For each node that has been placed in the matrix at position
res[r][c], place its left child atres[r+1][c-2height-r-1]and its right child atres[r+1][c+2height-r-1]. - Continue this process until all the nodes in the tree have been placed.
- Any empty cells should contain the empty string
"".
Return the constructed matrix res.
Example 1:
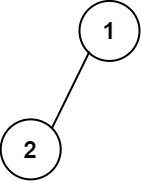
Input: root = [1,2] Output: [["","1",""], ["2","",""]]
Example 2:
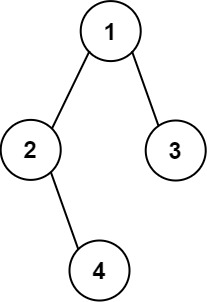
Input: root = [1,2,3,null,4] Output: [["","","","1","","",""], ["","2","","","","3",""], ["","","4","","","",""]]
Constraints:
- The number of nodes in the tree is in the range
[1, 210]. -99 <= Node.val <= 99- The depth of the tree will be in the range
[1, 10].
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What data type are the node values in the binary tree, and what range of values can they take? Can they be null or negative?
- What output format are you expecting? Should I return a list of lists representing each level, or a string representation?
- If the tree is empty (i.e., the root is null), what should the output be?
- Do you have any preference on the order of nodes at each level (e.g., left-to-right or right-to-left)?
- Is it a binary search tree, or a general binary tree?
Brute Force Solution
Approach
The basic idea is to represent the tree as a grid of text and fill in the nodes level by level. We will try every possible position for each node in the tree to find the best fit. This is a very simple and inefficient way to print the tree.
Here's how the algorithm would work step-by-step:
- First, create a big empty grid, like a large piece of graph paper, that will hold our tree's printed representation.
- Start at the root of the tree and try placing it at every possible spot in the middle of the top row of the grid.
- For each possible position of the root, figure out where its children would go, trying all possibilities for their placements on the next row down.
- Keep doing this for all the children and their children, exploring every single possible arrangement of nodes within the grid.
- For each full arrangement that we try, check to see if any nodes overlap or if the spacing between the nodes is too small.
- If an arrangement looks valid, we'll keep it around as a potential solution.
- After trying out every single possible arrangement, we'll look at all the valid ones we saved, and pick the one that looks the nicest based on things like even spacing and centering.
- Finally, print out the grid with the chosen arrangement of the tree.
Code Implementation
class Node:
def __init__(self, value, left=None, right=None):
self.value = value
self.left = left
self.right = right
def print_binary_tree_brute_force(root):
if not root:
return
# Determine tree height for grid size
tree_height = get_tree_height(root)
grid_width = 2**(tree_height - 1) * 2 - 1
grid_height = tree_height
# Initialize the grid with empty strings
grid = [['' for _ in range(grid_width)] for _ in range(grid_height)]
all_arrangements = []
def explore_arrangements(node, row, col, current_arrangement):
if not node:
return
# Try placing the node at the current position
current_arrangement[row][col] = str(node.value)
#Explore subtrees
left_col = col - 2**(tree_height - row - 2) if node.left else None
right_col = col + 2**(tree_height - row - 2) if node.right else None
if node.left:
explore_arrangements(node.left, row + 1, left_col, current_arrangement)
if node.right:
explore_arrangements(node.right, row + 1, right_col, current_arrangement)
def is_valid(arrangement):
# Check for overlaps in arrangement
for row in arrangement:
last_col = -1
for col_index, cell in enumerate(row):
if cell:
if last_col != -1 and col_index - last_col < 2:
return False
last_col = col_index
return True
def generate_arrangements(node, row):
if not node:
return []
valid_arrangements = []
for col in range(grid_width):
new_grid = [['' for _ in range(grid_width)] for _ in range(grid_height)]
explore_arrangements(node, row, col, new_grid)
if is_valid(new_grid):
valid_arrangements.append(new_grid)
return valid_arrangements
# Generate all possible valid arrangements
all_arrangements = generate_arrangements(root, 0)
# Pick the 'best' arrangement
best_arrangement = None
if all_arrangements:
best_arrangement = all_arrangements[0]
# Print the 'best' arrangement
if best_arrangement:
for row in best_arrangement:
print(''.join(['{:3}'.format(cell) for cell in row]))
else:
print("No valid arrangement found.")
def get_tree_height(node):
if not node:
return 0
return 1 + max(get_tree_height(node.left), get_tree_height(node.right))Big(O) Analysis
Optimal Solution
Approach
To print a binary tree in a structured way, we need to figure out each node's position in a grid. We'll use a smart approach that figures out the tree's dimensions and then fills the grid level by level, placing each node where it belongs.
Here's how the algorithm would work step-by-step:
- First, find out how tall and wide the tree is. The height tells us how many rows we need, and the width tells us how many columns.
- Create an empty grid (like a spreadsheet) with the right number of rows and columns. Fill every spot with an empty string to start.
- Start at the very top (root) of the tree and put its value in the middle of the first row of your grid.
- Now, look at the nodes on the next level down. The left child of the top node goes to the left of its parent in the next row, and the right child goes to the right.
- Continue this process for each level of the tree, filling in the values of the nodes in the correct places in the grid.
- If a node doesn't exist (it's empty), just leave its spot in the grid empty as well.
- Once you've filled in the entire grid, print each row to get your formatted tree.
Code Implementation
def print_binary_tree(root):
def get_tree_height(node):
if not node:
return 0
return 1 + max(get_tree_height(node.left), get_tree_height(node.right))
def get_tree_width(height):
return 2**height - 1
height_of_tree = get_tree_height(root)
width_of_tree = get_tree_width(height_of_tree)
tree_grid = [[''] * width_of_tree for _ in range(height_of_tree)]
def populate_grid(node, row, left, right):
if not node:
return
mid = (left + right) // 2
tree_grid[row][mid] = str(node.val)
# Recursively populate the left subtree.
populate_grid(node.left, row + 1, left, mid - 1)
# Recursively populate the right subtree.
populate_grid(node.right, row + 1, mid + 1, right)
# Populate the grid starting from the root.
populate_grid(root, 0, 0, width_of_tree - 1)
for row in tree_grid:
print(''.join(row))
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = rightBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty tree | Return an empty list immediately, as there is nothing to print. |
| Tree with only a root node | Print the root node's value in a list containing just that value. |
| Completely unbalanced tree (left-skewed) | The algorithm should still correctly print the tree, although the visual layout might be very wide if a level-order traversal is used. |
| Completely unbalanced tree (right-skewed) | Similar to the left-skewed case, the algorithm should handle it correctly but with potential visual layout issues. |
| Tree with duplicate values | The printing algorithm should handle duplicate values without issues, printing each instance of the value as it appears in the tree's structure. |
| Tree with negative values | The algorithm should be able to handle nodes with negative values. |
| Very large tree (potential stack overflow with recursion) | If using a recursive approach, consider the stack depth and potentially switch to an iterative approach like level-order traversal to prevent stack overflow. |
| Integer overflow in node values (if applicable to the problem context) | Be mindful of potential integer overflows when performing calculations with node values and use appropriate data types or overflow checks. |