Same Tree
EasyGiven the roots of two binary trees p and q, write a function to check if they are the same or not.
Two binary trees are considered the same if they are structurally identical, and the nodes have the same value.
Example 1:
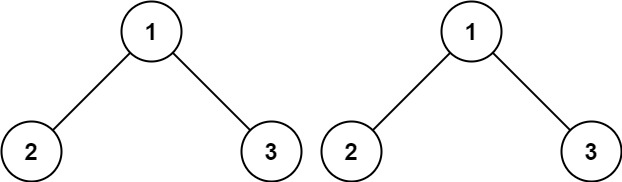
Input: p = [1,2,3], q = [1,2,3] Output: true
Example 2:
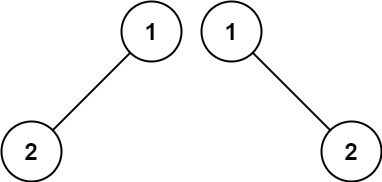
Input: p = [1,2], q = [1,null,2] Output: false
Example 3:

Input: p = [1,2,1], q = [1,1,2] Output: false
Constraints:
- The number of nodes in both trees is in the range
[0, 100]. -104 <= Node.val <= 104
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can the binary tree nodes contain any data type, or are they specifically integers?
- What is the range of possible values for the node values?
- Can either `p` or `q` be null or empty trees, and how should that be handled?
- By 'structurally identical', do you mean the trees must have the exact same shape, including the placement of null nodes?
- Should the function return `true` or `false` (or some other value) if both input trees are null?
Brute Force Solution
Approach
The brute force method for checking if two trees are the same involves directly comparing every single part of one tree with the corresponding part of the other tree. It is like meticulously going through a checklist for each tree to see if they are absolutely identical. If any difference is found, we immediately know they are not the same.
Here's how the algorithm would work step-by-step:
- First, check if both trees are completely empty. If they are, they are the same.
- Next, if only one tree is empty while the other is not, they are different.
- If both trees have values at their starting points, compare these values. If they're different, the trees are different.
- If the starting values are the same, then we must check the left side of both trees in the exact same way. Treat the left sides as if they are smaller trees and start this whole process over.
- If the left sides are the same, then we must also check the right side of both trees in the same way. Again, treat the right sides as smaller trees and repeat the whole process.
- The trees are considered the same only if every corresponding value and every corresponding structure, from the very top to the very bottom, matches exactly.
Code Implementation
def is_same_tree(tree_one, tree_two):
# Check if both trees are empty.
if not tree_one and not tree_two:
return True
# Check if only one tree is empty.
if not tree_one or not tree_two:
return False
# Compare the values of the root nodes.
if tree_one.val != tree_two.val:
return False
# Recursively check the left subtrees.
left_trees_are_same = is_same_tree(tree_one.left, tree_two.left)
# If left trees aren't the same, overall not the same
if not left_trees_are_same:
return False
# Recursively check the right subtrees.
right_trees_are_same = is_same_tree(tree_one.right, tree_two.right)
return right_trees_are_sameBig(O) Analysis
Optimal Solution
Approach
The best way to check if two trees are the same is to compare them piece by piece, simultaneously. We'll go down both trees at the same time, checking if each corresponding part matches up, and if not, immediately conclude they are different.
Here's how the algorithm would work step-by-step:
- First, check if both trees are empty. If they are, then they are the same.
- If only one of the trees is empty, they can't be the same, so say they are different.
- If both trees have a top part, compare the values of these parts. If they are different, the trees are different.
- If the top parts are the same, then we need to check if the left parts of the trees are the same using this exact same process.
- Then, we need to check if the right parts of the trees are the same, again using the exact same process.
- If the top parts, the left parts, and the right parts are all the same, then the trees are the same.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def is_same_tree(tree_one, tree_two):
# If both trees are empty, they are identical.
if not tree_one and not tree_two:
return True
# If only one tree is empty, they cannot be identical.
if not tree_one or not tree_two:
return False
# If the values of the current nodes are different, trees differ.
if tree_one.val != tree_two.val:
return False
# Recursively check if the left subtrees are the same.
left_subtree_is_same = is_same_tree(tree_one.left, tree_two.left)
# Recursively check if the right subtrees are the same.
right_subtree_is_same = is_same_tree(tree_one.right, tree_two.right)
# The trees are the same if both subtrees are the same.
return left_subtree_is_same and right_subtree_is_sameBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Both input trees are null | Return true, as two null trees are considered identical. |
| One tree is null, and the other is not null | Return false, as one tree having nodes while the other is empty means they are different. |
| Trees have different structures (different shapes), but the same values at corresponding nodes up to a point | The recursive or iterative check will eventually reach differing structural parts, returning false. |
| Trees have identical structure, but different values at one or more nodes | The value comparison within the recursive/iterative logic will identify the mismatch, returning false. |
| Large trees exceeding recursion depth limits (stack overflow) | Consider using an iterative approach (e.g., with a stack) to avoid recursion depth limitations. |
| Trees with only one node each, but different values | The root value comparison will immediately detect the difference, returning false. |
| Trees with only one node each, and the same values | The root value comparison will confirm equality, and since no further nodes exist, it returns true. |
| Trees with negative, zero, and positive integer values in their nodes | The standard integer comparison will handle all these value types correctly without special treatment. |