Shortest Distance After Road Addition Queries I

Medium

Asked by:

5 views

Topics:

GraphsDynamic Programming

You are given an integer n and a 2D integer array queries.

There are n cities numbered from 0 to n - 1. Initially, there is a unidirectional road from city i to city i + 1 for all 0 <= i < n - 1.

queries[i] = [u_i, v_i] represents the addition of a new unidirectional road from city u_i to city v_i. After each query, you need to find the length of the shortest path from city 0 to city n - 1.

Return an array answer where for each i in the range [0, queries.length - 1], answer[i] is the length of the shortest path from city 0 to city n - 1 after processing the first i + 1 queries.

Example 1:

Input: n = 5, queries = [[2,4],[0,2],[0,4]]

Output: [3,2,1]

Explanation:

After the addition of the road from 2 to 4, the length of the shortest path from 0 to 4 is 3.

After the addition of the road from 0 to 2, the length of the shortest path from 0 to 4 is 2.

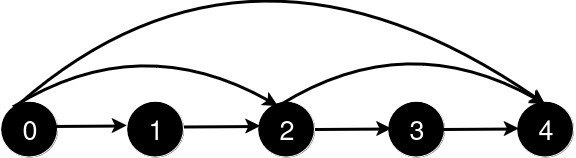
After the addition of the road from 0 to 4, the length of the shortest path from 0 to 4 is 1.

Example 2:

Input: n = 4, queries = [[0,3],[0,2]]

Output: [1,1]

Explanation:

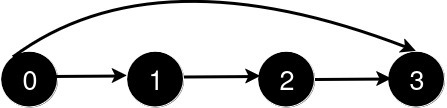
After the addition of the road from 0 to 3, the length of the shortest path from 0 to 3 is 1.

After the addition of the road from 0 to 2, the length of the shortest path remains 1.

Constraints:

3 <= n <= 500
1 <= queries.length <= 500
queries[i].length == 2
0 <= queries[i][0] < queries[i][1] < n
1 < queries[i][1] - queries[i][0]
There are no repeated roads among the queries.

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the maximum values for `n` (number of nodes), `edges.length`, and `queries.length`? What is the maximum weight for an edge?
Are edge weights guaranteed to be non-negative?
Are the node indices 0-based or 1-based?
If adding a road in a query results in a graph that is still disconnected, what should the shortest distance between the specified nodes be?
If there are multiple shortest paths between two nodes, is any of them acceptable?

Brute Force Solution

Approach

Imagine you have a map with cities and roads, and you want to find the shortest way to get from one city to another. We start with some roads, then add more roads one at a time. The brute force approach is like re-calculating the shortest path from start to end after each new road is added.

Here's how the algorithm would work step-by-step:

First, consider the map with the original roads. Figure out the shortest path between the start and end cities using only those roads.
Now, add the first new road to the map.
Re-calculate the shortest path between the start and end cities, this time using all the original roads AND the new road you just added. Explore every possible route to be sure.
Repeat this process for each new road that is added. Each time, you need to re-calculate the shortest path from scratch, considering all the roads that are currently on the map.
After adding each new road and recalculating the shortest path, save that shortest path distance. This gives you a list of the shortest distances after each road addition.

Code Implementation

import heapq

def shortest_distance_after_road_additions_i(
    number_of_nodes, edges, queries, source_node, destination_node
):

    results = []
    current_edges = edges[:]  # Start with the initial edges

    for query in queries:
        current_edges.append(query)

        # Calculate shortest path after adding the road
        distance = dijkstra(
            number_of_nodes, current_edges, source_node, destination_node
        )
        results.append(distance if distance != float('inf') else -1)

    return results

def dijkstra(number_of_nodes, edges, source_node, destination_node):
    graph = {i: [] for i in range(number_of_nodes)}
    for source, destination, weight in edges:
        graph[source].append((destination, weight))

    distances = {i: float('inf') for i in range(number_of_nodes)}
    distances[source_node] = 0
    priority_queue = [(0, source_node)]  # (distance, node)

    while priority_queue:
        current_distance, current_node = heapq.heappop(priority_queue)

        if current_distance > distances[current_node]:
            continue

        for neighbor, weight in graph[current_node]:
            distance = current_distance + weight

            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(priority_queue, (distance, neighbor))

    return distances[destination_node]

Big(O) Analysis

Time Complexity

O(m * n^2 * log n) – The algorithm processes m road addition queries. After each addition, it recalculates the shortest path between the start and end nodes using Dijkstra's algorithm. Dijkstra's algorithm, implemented with a priority queue, typically has a time complexity of O(n log n) where n is the number of nodes. However, each time Dijkstra's is run, we consider up to n edges (roads) and in worst case, Dijkstra's algorithm may visit each edge, so this introduces an additional factor of n. Thus, for m queries, we have m * (n * (n log n)), which simplifies to O(m * n^2 * log n).

Space Complexity

O(N^2) – The brute force approach recalculates the shortest path from scratch after each road addition. This likely involves using an adjacency matrix or list to represent the graph, whose size is proportional to the number of nodes (cities), N, squared. Since we need to store the graph representation at each step, the space complexity will be at least O(N^2). Temporary data structures for shortest path algorithms like Dijkstra's or Floyd-Warshall could also contribute, but the graph representation dominates. Hence, the overall auxiliary space complexity is O(N^2).

Optimal Solution

Approach

We want to find the shortest paths between all pairs of locations as we add new roads. A clever approach involves updating shortest path distances only when a new road might create a shorter route between two locations, rather than recalculating everything from scratch each time.

Here's how the algorithm would work step-by-step:

Start with the initial road network and calculate the shortest distance between every pair of locations using a known algorithm (imagine a map showing the quickest way to get from each city to every other city).
When a new road is added, consider all possible pairs of locations.
For each pair, check if the new road creates a shorter path between them. This means seeing if going from one location to the road, then along the road, and then from the road to the other location is faster than the current shortest path.
If the new road does create a shorter path, update the shortest distance between those locations.
Repeat this process for every new road added.
The trick is to only update distances that might be affected by the new road, avoiding recalculating everything, which would take much longer.

Code Implementation

def shortest_distance_after_road_addition(number_of_locations, edges, queries):
    distance_matrix = [[float('inf')] * number_of_locations for _ in range(number_of_locations)]

    for i in range(number_of_locations):
        distance_matrix[i][i] = 0

    for source, destination, weight in edges:
        distance_matrix[source][destination] = weight
        distance_matrix[destination][source] = weight

    # Initialize shortest paths using Floyd-Warshall
    for intermediate in range(number_of_locations):
        for source in range(number_of_locations):
            for destination in range(number_of_locations):
                distance_matrix[source][destination] = min(
                    distance_matrix[source][destination],
                    distance_matrix[source][intermediate] + distance_matrix[intermediate][destination]
                )

    results = []

    for source, destination, weight in queries:
        # Adding a new road, check for possible shortest paths
        for start_node in range(number_of_locations):
            for end_node in range(number_of_locations):
                # Checking if new road provides a shorter path
                distance_matrix[start_node][end_node] = min(
                    distance_matrix[start_node][end_node],
                    distance_matrix[start_node][source] + weight + distance_matrix[destination][end_node],
                    distance_matrix[start_node][destination] + weight + distance_matrix[source][end_node]
                )
        shortest_distance = [[float('inf')] * number_of_locations for _ in range(number_of_locations)]
        for i in range(number_of_locations):
            shortest_distance[i][i] = 0

        for start_node in range(number_of_locations):
            for end_node in range(number_of_locations):
                shortest_distance[start_node][end_node] = distance_matrix[start_node][end_node]
        results.append(shortest_distance)

    return results

Big(O) Analysis

Time Complexity

O(n² * q) – Let n be the number of locations (nodes). We first calculate the initial all-pairs shortest paths, which can be done in O(n³) time (e.g., using Floyd-Warshall). However, the core of this question focuses on the update step after each road addition. For each of the q queries (road additions), we iterate through all possible pairs of locations (nodes), which takes O(n²) time. For each pair, we check if going through the new road yields a shorter path. Therefore, each query takes O(n²) time, and with q queries, the total time complexity becomes O(n² * q), assuming the initial all-pairs shortest path calculation is precomputed or has lower complexity than O(n² * q).

Space Complexity

O(N^2) – The algorithm starts by calculating the shortest distance between every pair of locations, which requires storing these distances. This is typically done using a matrix (or similar data structure) of size N x N, where N is the number of locations. The addition of new roads only updates this matrix, but does not fundamentally alter its size. Therefore, the auxiliary space is dominated by the N x N distance matrix, leading to O(N^2) space complexity.

Edge Cases

Case	How to Handle
Null or empty road network (n=0 or queries is null/empty)	Return an empty list immediately, as there are no distances to calculate.
Single node graph (n=1) with queries	Return a list of all -1s because there are no other nodes to calculate the shortest distance to.
Queries that add edges creating a disconnected graph	Shortest path calculation should return -1 for nodes in separate components.
Queries add edges creating cycles in the graph.	The shortest path algorithm (e.g., Floyd-Warshall) should correctly handle cycles without infinite loops.
Maximum number of nodes and edges allowed by the problem constraints (potential memory issues).	Ensure that the adjacency matrix or other data structures used to represent the graph do not exceed available memory.
Integer overflow in distance calculations (especially with many edges).	Use a data type that can accommodate large distances (e.g., long) and check for overflow during calculations.
Queries that add duplicate edges.	Adding a duplicate edge should not change the shortest path; the algorithm handles it by updating the distance only if the new edge reduces it.
No path exists between certain node pairs even after all roads added.	The shortest path algorithm should return -1 for these node pairs.

Null or empty road network (n=0 or queries is null/empty)

How to Handle:

Return an empty list immediately, as there are no distances to calculate.

Single node graph (n=1) with queries

How to Handle:

Return a list of all -1s because there are no other nodes to calculate the shortest distance to.

Queries that add edges creating a disconnected graph

How to Handle:

Shortest path calculation should return -1 for nodes in separate components.

Queries add edges creating cycles in the graph.

How to Handle:

The shortest path algorithm (e.g., Floyd-Warshall) should correctly handle cycles without infinite loops.

Maximum number of nodes and edges allowed by the problem constraints (potential memory issues).

How to Handle:

Ensure that the adjacency matrix or other data structures used to represent the graph do not exceed available memory.

Integer overflow in distance calculations (especially with many edges).

How to Handle:

Use a data type that can accommodate large distances (e.g., long) and check for overflow during calculations.

Queries that add duplicate edges.

How to Handle:

Adding a duplicate edge should not change the shortest path; the algorithm handles it by updating the distance only if the new edge reduces it.

No path exists between certain node pairs even after all roads added.

How to Handle:

The shortest path algorithm should return -1 for these node pairs.