Symmetric Tree
EasyGiven the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).
Example 1:
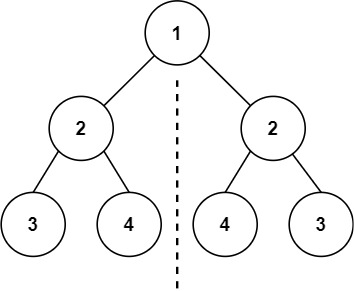
Input: root = [1,2,2,3,4,4,3] Output: true
Example 2:
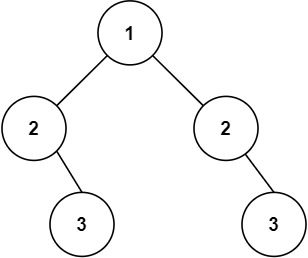
Input: root = [1,2,2,null,3,null,3] Output: false
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. -100 <= Node.val <= 100
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the constraints on the number of nodes in the tree, and what is the range of values for the node data?
- Can the tree be empty (i.e., `root` is null)? If so, what should be returned?
- Are node values guaranteed to be unique, or can duplicate values exist in the tree?
- Does the definition of symmetry require the *values* of the mirrored nodes to be equal, or is it purely structural symmetry?
- If the tree is not symmetric, is there a specific return value (e.g., `false` or an empty structure) expected, or should we assume a boolean return?
Brute Force Solution
Approach
To check if a tree is symmetric, we can compare its left side with its right side. The brute force approach involves systematically checking if the corresponding parts of the left and right halves mirror each other perfectly.
Here's how the algorithm would work step-by-step:
- Take the very center of the tree, the root node itself.
- Look at the left child of the root and the right child of the root.
- If one exists and the other doesn't, the tree isn't symmetric.
- If both exist, compare what's on the immediate left of the left child with what's on the immediate right of the right child.
- Also, compare what's on the immediate right of the left child with what's on the immediate left of the right child.
- If these pairs don't match, the tree isn't symmetric.
- If they do match, continue this process outwards, comparing pairs of nodes that should mirror each other.
- Keep doing this, step by step, moving deeper into the tree, until you've checked every corresponding pair of nodes.
- If all pairs match all the way down, then the tree is symmetric.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.value = val
self.left_child = left
self.right_child = right
def is_symmetric(root_node):
if not root_node:
return True
return check_mirror_subtrees(root_node.left_child, root_node.right_child)
def check_mirror_subtrees(left_subtree_node, right_subtree_node):
# If both nodes are null, they are symmetric counterparts
if not left_subtree_node and not right_subtree_node:
return True
# If one node exists and the other doesn't, they are not symmetric
if not left_subtree_node or not right_subtree_node:
return False
# If the values of the current nodes don't match, they are not symmetric
if left_subtree_node.value != right_subtree_node.value:
return False
# Recursively check the outer children and the inner children
return (check_mirror_subtrees(left_subtree_node.left_child, right_subtree_node.right_child) and
check_mirror_subtrees(left_subtree_node.right_child, right_subtree_node.left_child))Big(O) Analysis
Optimal Solution
Approach
To check if a tree is symmetric, we need to compare its left side with its right side in a mirrored fashion. The core idea is to simultaneously traverse both halves of the tree, ensuring that corresponding nodes have the same value and are positioned symmetrically.
Here's how the algorithm would work step-by-step:
- Imagine you have the tree. Pick the very center of the tree, which is the root. This is our starting point.
- Now, think about the two children of the root: the left child and the right child. These will be the starting points for our mirrored comparison.
- We'll compare the left child of the left side with the right child of the right side. They must match.
- We'll also compare the right child of the left side with the left child of the right side. These must also match.
- If at any point we expect to find a node in one half, but there isn't a corresponding node in the other half, the tree isn't symmetric.
- Also, if we find nodes at corresponding mirrored positions, but their values are different, the tree isn't symmetric.
- We continue this process, working outwards from the root, comparing pairs of nodes that are mirror images of each other.
- If we can go through the entire tree comparing these mirrored pairs and find that they all match perfectly, then the tree is symmetric.
Code Implementation
class TreeNode:
def __init__(self, value=0, left=None, right=None):
self.value = value
self.left = left
self.right = right
def is_symmetric_tree(root_node):
if not root_node:
return True
def check_mirrored_subtrees(left_subtree_node, right_subtree_node):
# If both nodes are null, they are considered symmetric.
if not left_subtree_node and not right_subtree_node:
return True
# If one node is null but the other isn't, they are not symmetric.
if not left_subtree_node or not right_subtree_node:
return False
# Values must match for symmetric nodes.
if left_subtree_node.value != right_subtree_node.value:
return False
# Recursively check the outer pair (left's left and right's right).
# Then recursively check the inner pair (left's right and right's left).
return (check_mirrored_subtrees(left_subtree_node.left, right_subtree_node.right) and
check_mirrored_subtrees(left_subtree_node.right, right_subtree_node.left))
# Start the mirrored comparison from the children of the root node.
return check_mirrored_subtrees(root_node.left, root_node.right)Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| An empty tree (root is null) | An empty tree is considered symmetric, so the solution should return true immediately. |
| A tree with only a root node | A single node tree is symmetric by definition, and the recursive comparison should handle this base case correctly. |
| A tree with only a left child or only a right child | These are not symmetric and should be identified as false by comparing a non-null node with a null node. |
| A tree with perfect symmetry | The recursive or iterative approach should correctly traverse and compare all mirrored nodes. |
| A tree that is not symmetric at any level | The comparison function should detect the first asymmetry and return false promptly. |
| A tree with identical values at mirrored positions but structurally different | The structural comparison (left child of left subtree vs. right child of right subtree) is crucial and should be handled. |
| Very deep trees that could lead to stack overflow with recursion | An iterative approach using a queue or stack would mitigate potential stack overflow issues for extremely deep trees. |
| Trees with large numbers of nodes | The solution's time complexity should be O(N) and space complexity O(H) (or O(N) in worst case for iterative), which is efficient for large trees. |