Maximum Level Sum of a Binary Tree
MediumGiven the root of a binary tree, the level of its root is 1, the level of its children is 2, and so on.
Return the smallest level x such that the sum of all the values of nodes at level x is maximal.
Example 1:
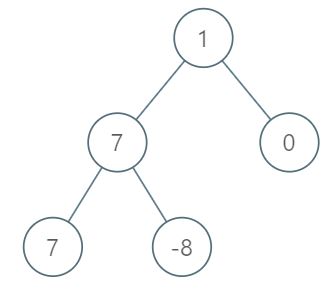
Input: root = [1,7,0,7,-8,null,null] Output: 2 Explanation: Level 1 sum = 1. Level 2 sum = 7 + 0 = 7. Level 3 sum = 7 + -8 = -1. So we return the level with the maximum sum which is level 2.
Example 2:
Input: root = [989,null,10250,98693,-89388,null,null,null,-32127] Output: 2
Constraints:
- The number of nodes in the tree is in the range
[1, 104]. -105 <= Node.val <= 105
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for the node values in the binary tree? Can they be negative, zero, or floating-point numbers?
- What should I return if the tree is empty or null?
- In the case of multiple levels having the same maximum sum, should I return the smallest (topmost) level number or the largest?
- What is the maximum depth of the tree that I should expect?
- Is the tree guaranteed to be a valid binary tree, or do I need to handle cases where the tree structure is malformed (e.g., cycles)?
Brute Force Solution
Approach
The brute-force way to find the level with the maximum sum in a tree involves calculating the sum of each level individually. We'll go through the tree level by level, compute the sum for that level, and keep track of the largest sum we've seen so far and the level it occurred on.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree, which is level 1.
- Calculate the sum of all the node values on that level.
- Store the sum and the level number.
- Move down to the next level (level 2).
- Calculate the sum of all node values on this level.
- Compare the current level's sum with the largest sum we've stored so far.
- If the current level's sum is bigger, replace the stored sum and the corresponding level with the current level's sum and level number.
- Repeat steps 4-7 for each level of the tree, going down one level at a time.
- Once you've reached the bottom of the tree, the stored level number will be the level with the maximum sum.
Code Implementation
def max_level_sum(root):
if not root:
return 0
maximum_level_sum = float('-inf')
level_with_maximum_sum = 0
current_level = 1
nodes_at_current_level = [root]
while nodes_at_current_level:
level_sum = 0
next_level_nodes = []
for node in nodes_at_current_level:
level_sum += node.val
if node.left:
next_level_nodes.append(node.left)
if node.right:
next_level_nodes.append(node.right)
#Compare current level's sum to the max
if level_sum > maximum_level_sum:
maximum_level_sum = level_sum
level_with_maximum_sum = current_level
#Move to the next level
nodes_at_current_level = next_level_nodes
current_level += 1
return level_with_maximum_sumBig(O) Analysis
Optimal Solution
Approach
The goal is to find the level in a tree with the highest sum. We do this by systematically visiting each level of the tree and calculating the sum of the nodes at that level, keeping track of the level with the maximum sum found so far.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree (the root).
- Imagine processing the tree level by level, like reading lines in a book.
- For each level, add up the values of all the tree parts (nodes) at that level.
- Compare the sum you just calculated to the biggest sum you've seen so far.
- If the current level's sum is bigger, remember that sum and the current level number.
- Move down to the next level and repeat the summing and comparing process.
- Continue until you have processed all the levels of the tree.
- The level number associated with the biggest sum you remembered is your answer.
Code Implementation
def max_level_sum(root):
if not root:
return 0
maximum_sum = float('-inf')
maximum_sum_level = 0
current_level = 1
queue = [root]
while queue:
level_size = len(queue)
level_sum = 0
# Iterate through all nodes at the current level
for _ in range(level_size):
node = queue.pop(0)
level_sum += node.val
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
# Check if the current level sum is greater than the maximum sum
if level_sum > maximum_sum:
# Update the maximum sum and corresponding level
maximum_sum = level_sum
maximum_sum_level = current_level
current_level += 1
return maximum_sum_levelBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null root node (empty tree) | Return 0, as there are no levels to sum and therefore no maximum. |
| Tree with only one node (root) | Return 1, as the root is the only level and thus has the maximum sum. |
| Tree with highly skewed structure (e.g., all nodes on one branch) | BFS/Level Order Traversal handles skewed trees correctly by processing each level sequentially. |
| Tree with all nodes having negative values | The algorithm correctly identifies the level with the least negative (or largest negative) sum. |
| Tree with all nodes having zero values | Any level will be equally optimal, and the algorithm will return the first level encountered with sum 0. |
| Tree with both very large positive and very large negative values, leading to potential integer overflow during summation | Use long data type to accommodate large sums and prevent integer overflow. |
| A level with a very large number of nodes that might lead to memory exhaustion. | Memory is allocated and freed level by level in BFS, so it only needs to hold one level's worth of nodes in memory. |
| Maximum recursion depth exceeded in a recursive solution on a highly unbalanced tree. | Use BFS iterative solution instead of recursion to avoid stack overflow errors for unbalanced trees. |