Maximum Star Sum of a Graph

Medium

Amazon

4 views

Topics:

GraphsGreedy Algorithms

There is an undirected graph consisting of n nodes numbered from 0 to n - 1. You are given a 0-indexed integer array vals of length n where vals[i] denotes the value of the i^th node.

You are also given a 2D integer array edges where edges[i] = [a_i, b_i] denotes that there exists an undirected edge connecting nodes a_i and b_i.

A star graph is a subgraph of the given graph having a center node containing 0 or more neighbors. In other words, it is a subset of edges of the given graph such that there exists a common node for all edges.

The image below shows star graphs with 3 and 4 neighbors respectively, centered at the blue node.

The star sum is the sum of the values of all the nodes present in the star graph.

Given an integer k, return the maximum star sum of a star graph containing at most k edges.

Example 1:

Input: vals = [1,2,3,4,10,-10,-20], edges = [[0,1],[1,2],[1,3],[3,4],[3,5],[3,6]], k = 2
Output: 16
Explanation: The above diagram represents the input graph.
The star graph with the maximum star sum is denoted by blue. It is centered at 3 and includes its neighbors 1 and 4.
It can be shown it is not possible to get a star graph with a sum greater than 16.

Example 2:

Input: vals = [-5], edges = [], k = 0
Output: -5
Explanation: There is only one possible star graph, which is node 0 itself.
Hence, we return -5.

Constraints:

n == vals.length
1 <= n <= 10⁵
-10⁴ <= vals[i] <= 10⁴
0 <= edges.length <= min(n * (n - 1) / 2, 10⁵)
edges[i].length == 2
0 <= a_i, b_i <= n - 1
a_i != b_i
0 <= k <= n - 1

Maximum Star Sum of a Graph

Medium

Amazon

4 views

Topics:

GraphsGreedy Algorithms

There is an undirected graph consisting of n nodes numbered from 0 to n - 1. You are given a 0-indexed integer array vals of length n where vals[i] denotes the value of the i^th node.

You are also given a 2D integer array edges where edges[i] = [a_i, b_i] denotes that there exists an undirected edge connecting nodes a_i and b_i.

A star graph is a subgraph of the given graph having a center node containing 0 or more neighbors. In other words, it is a subset of edges of the given graph such that there exists a common node for all edges.

The image below shows star graphs with 3 and 4 neighbors respectively, centered at the blue node.

The star sum is the sum of the values of all the nodes present in the star graph.

Given an integer k, return the maximum star sum of a star graph containing at most k edges.

Example 1:

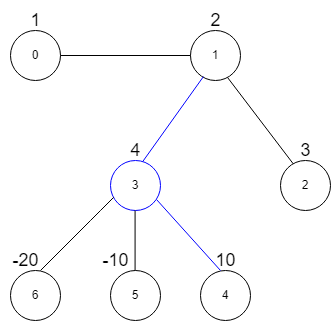
Input: vals = [1,2,3,4,10,-10,-20], edges = [[0,1],[1,2],[1,3],[3,4],[3,5],[3,6]], k = 2
Output: 16
Explanation: The above diagram represents the input graph.
The star graph with the maximum star sum is denoted by blue. It is centered at 3 and includes its neighbors 1 and 4.
It can be shown it is not possible to get a star graph with a sum greater than 16.

Example 2:

Input: vals = [-5], edges = [], k = 0
Output: -5
Explanation: There is only one possible star graph, which is node 0 itself.
Hence, we return -5.

Constraints:

n == vals.length
1 <= n <= 10⁵
-10⁴ <= vals[i] <= 10⁴
0 <= edges.length <= min(n * (n - 1) / 2, 10⁵)
edges[i].length == 2
0 <= a_i, b_i <= n - 1
a_i != b_i
0 <= k <= n - 1

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the possible ranges for the values in the `vals` array, and can they be negative, zero, or positive?
What are the constraints on the number of nodes `n` and the number of edges in the `edges` array? Is there a maximum number of edges?
If the `edges` array is empty, what should be returned? Similarly, if a node has no neighbors, what should its 'star sum' be?
Are there any constraints on the maximum degree of a node? Can I assume the graph is connected?
If multiple 'stars' yield the same maximum sum, is any one of them acceptable, or is there a specific criterion for choosing among them?

Brute Force Solution

Approach

The brute force strategy involves examining every possible 'star' within the graph to find the one with the largest sum. We consider each node as the center of a potential star and then explore all its neighbors to find the arrangement yielding the highest sum.

Here's how the algorithm would work step-by-step:

For every node in the graph, consider it as the center of a potential star.
For each center node, consider all possible combinations of its neighbors.
Calculate the sum of the center node's value and the values of the chosen neighbors for each combination.
Keep track of the largest sum found so far.
After considering all nodes as centers and all combinations of their neighbors, the largest sum recorded is the maximum star sum.

Code Implementation

def max_star_sum_brute_force(values, edges):
    maximum_star_sum = float('-inf')
    number_of_nodes = len(values)

    # Iterate through each node to consider it as the center of the star.
    for center_node in range(number_of_nodes):
        neighbor_nodes = []

        for edge in edges:
            if edge[0] == center_node:
                neighbor_nodes.append(edge[1])
            elif edge[1] == center_node:
                neighbor_nodes.append(edge[0])

        # Consider all possible combinations of neighbors.
        number_of_neighbors = len(neighbor_nodes)
        for i in range(1 << number_of_neighbors):
            current_star_sum = values[center_node]
            neighbors_in_star = []

            for j in range(number_of_neighbors):
                # Choose only neighbors where the j-th bit is set.
                if (i >> j) & 1:
                    neighbors_in_star.append(neighbor_nodes[j])

            for neighbor_node in neighbors_in_star:
                current_star_sum += values[neighbor_node]

            # Update the global maximum star sum if needed.
            maximum_star_sum = max(maximum_star_sum, current_star_sum)

    return maximum_star_sum

Big(O) Analysis

Time Complexity

O(n * 2^d) – The algorithm iterates through each of the n nodes in the graph, considering each as a potential center of a star. For each center node, it examines all possible combinations of its neighbors. In the worst-case scenario, a node could be connected to d other nodes (neighbors), where d is the maximum degree of any node in the graph. Evaluating all combinations of neighbors for a single center node requires considering 2^d possible subsets. Therefore, the overall time complexity is O(n * 2^d), where n is the number of nodes and d is the maximum degree of any node. While d could potentially approach n in a dense graph, it's important to note that this is an upper bound, and the actual time taken will depend on the graph's structure.

Space Complexity

O(1) – The described brute force algorithm examines each node and its neighbors. It primarily involves calculating sums and comparing them to find the maximum. The algorithm doesn't explicitly mention creating auxiliary data structures like lists, hash maps, or recursion. Thus, the space used to store intermediate sums and the current maximum sum is constant, irrespective of the graph's size (number of nodes and edges). Therefore, the space complexity is O(1).

Optimal Solution

Approach

The core idea is to find the node that, when connected to its 'best' neighbors, results in the highest possible sum. We focus on the nodes with the most positive connections, as negative connections reduce the overall sum. We can use a simple strategy that doesn't require checking every single possible group of connections.

Here's how the algorithm would work step-by-step:

For each node in the graph, identify its neighboring nodes and the associated values (connection strengths).
Sort the neighbors of each node based on their connection strength, from strongest (most positive) to weakest (most negative).
Select the 'k' strongest neighbors for each node, where 'k' is a given limit on the number of connections.
Calculate the 'star sum' for each node by adding its own value to the sum of the values of its selected strongest neighbors.
Keep track of the highest star sum encountered so far.
After examining all nodes, the highest star sum recorded is the answer.

Code Implementation

def maximum_star_sum(node_values, edges, max_number_of_nodes):
    number_of_nodes = len(node_values)
    adjacency_list = [[] for _ in range(number_of_nodes)]

    for start_node, end_node in edges:
        adjacency_list[start_node].append(end_node)
        adjacency_list[end_node].append(start_node)

    max_star_sum_so_far = float('-inf')

    for current_node in range(number_of_nodes):
        # Need to filter nodes based on connection values
        neighbor_values = []
        for neighbor_node in adjacency_list[current_node]:
            neighbor_values.append(node_values[neighbor_node])

        neighbor_values.sort(reverse=True)

        current_star_sum = node_values[current_node]
        number_of_neighbors_to_add = min(max_number_of_nodes, len(neighbor_values))

        # Only add neighbors that contribute positively
        for i in range(number_of_neighbors_to_add):
            if neighbor_values[i] > 0:
                current_star_sum += neighbor_values[i]
            else:
                break

        max_star_sum_so_far = max(max_star_sum_so_far, current_star_sum)

    return max_star_sum_so_far

Big(O) Analysis

Time Complexity

O(n log n) – The algorithm iterates through each node in the graph, which takes O(n) time where n is the number of nodes. Inside the loop for each node, the neighbors are sorted based on their connection strengths. Sorting the neighbors takes O(degree * log(degree)) time, where degree is the number of neighbors of the node. In the worst case, the degree can be proportional to n. Therefore, the sorting step contributes O(n log n) in the worst case for each node. Summing over all nodes, the total time complexity is dominated by the sorting steps resulting in O(n * n log n) if the graph is fully connected, and O(n log n) if the graph is sparse since the degree value will generally be smaller than n. After examining all nodes the algorithm finds the max, which also takes O(n) time, but it is dominated by the sorting complexity.

Space Complexity

O(N) – The primary auxiliary space usage comes from storing the neighbors of each node. In the worst-case scenario, a node might be connected to all other nodes in the graph. This means we need to store a list of neighbors for each node, and the total space required to store all these lists could be proportional to the number of nodes N (where N is the number of nodes in the graph). Therefore, the space complexity is O(N) because we store neighbors for each node to find the k strongest neighbors.

Edge Cases

Case	How to Handle
Null or empty graph (no nodes or edges)	Return 0, as there are no stars to sum.
Graph with only one node	Return the value of the single node since a star requires at least one edge.
Graph with no edges	Return the maximum value node, as each node is a star with sum equal to its own value.
All node values are negative	If k > 0, return the largest negative value; if k = 0, return the largest negative value.
Nodes with extremely large positive or negative values (potential integer overflow)	Use a data type that can accommodate large values (e.g., long) to prevent overflow during summation.
k is zero (only the central node's value is counted)	Iterate through the node values and return the maximum node value.
Nodes with duplicate values	The algorithm should handle duplicate node values correctly without affecting the maximum star sum calculation.
k is larger than the number of neighbors of any node	Only sum as many neighbors as the node has when k is larger than the number of neighbors of a node.