N-ary Tree Preorder Traversal
EasyGiven the root of an n-ary tree, return the preorder traversal of its nodes' values.
Nary-Tree input serialization is represented in their level order traversal. Each group of children is separated by the null value (See examples)
Example 1:
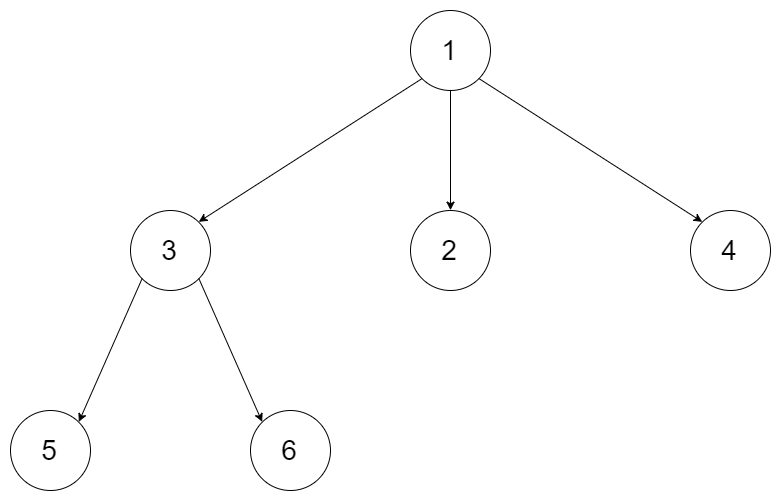
Input: root = [1,null,3,2,4,null,5,6] Output: [1,3,5,6,2,4]
Example 2:
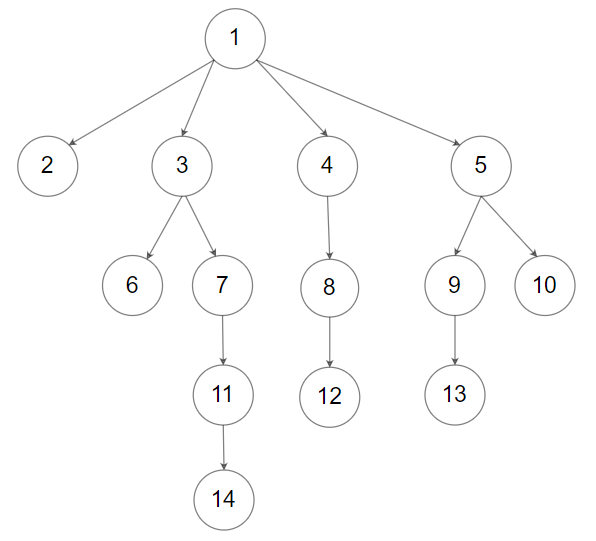
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] Output: [1,2,3,6,7,11,14,4,8,12,5,9,13,10]
Constraints:
- The number of nodes in the tree is in the range
[0, 104]. 0 <= Node.val <= 104- The height of the n-ary tree is less than or equal to
1000.
Follow up: Recursive solution is trivial, could you do it iteratively?
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can the tree be empty (null)? What should I return in that case?
- What is the range of values for the 'val' property of each node? Can it be negative?
- How is the N-ary tree represented? Specifically, what data structure is used for the 'children' array/list?
- Is the order of children in the 'children' array significant for the purpose of traversal?
- What should I return? Is it just a list of node values (integers) in preorder, or do I need to return Node objects?
Brute Force Solution
Approach
The brute force method for traversing a tree in preorder means visiting the nodes in a very specific, but simple way. We'll start at the very top, process that node, and then handle each of its children from left to right, fully exploring each child's subtree before moving on.
Here's how the algorithm would work step-by-step:
- First, we look at the very top node, which is called the root, and write down its value or do something with it.
- Then, we look at the first child of the root node.
- We treat that first child like a new root and apply the exact same process: write down its value.
- Then, we look at the first child of that child node and repeat the process until we have no more children to explore down that path.
- Once we've gone as far down as we can on the first child's branch, we go back up one level and look at the next child of the node we were just at.
- We repeat the process of exploring each child's branch from left to right until we have visited every node in the entire tree.
Code Implementation
class Node:
def __init__(self, value):
self.value = value
self.children = []
def n_ary_tree_preorder_traversal(root):
result_list = []
def traverse(node):
if not node:
return
result_list.append(node.value)
# Recursively call traverse on each child.
for child_node in node.children:
# Ensures each subtree is fully explored.
traverse(child_node)
traverse(root)
return result_listBig(O) Analysis
Optimal Solution
Approach
The best way to visit every node in an N-ary tree in preorder is to explore the tree one level at a time, starting from the root. We process each node and then visit all its children, ensuring we go deeper before moving to the next sibling. This is done by using a technique that remembers where we were so we can go back and process the other branches.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree, the root.
- Record the value of the current node because that's what 'preorder' means - process the node first.
- Look at the children of the current node, one by one.
- For each child, treat that child as the 'root' of a smaller tree and repeat the process - record its value and then visit its children.
- Keep going deeper and deeper into each branch until you reach a node with no children.
- Once you've gone as far down a branch as possible, go back to the last node that still had children that haven't been visited.
- Repeat steps 3-6 until you have visited every node in the entire tree.
Code Implementation
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children
class Solution:
def preorder(self, root: 'Node') -> list[int]:
result_list = []
def traverse_node(node: 'Node'):
if not node:
return
result_list.append(node.val)
# Visit each child in the order they appear
if node.children:
for child_node in node.children:
traverse_node(child_node)
# Recursively explore the subtree rooted at each child
traverse_node(root)
# Initiate the traversal from the root of the tree
return result_listBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty root node | Return an empty list immediately as there is no tree to traverse. |
| Tree with only the root node | Return a list containing only the value of the root node. |
| Tree with deeply nested children (high depth) | Iterative solution with a stack should be preferred over recursive to avoid stack overflow for extreme depths. |
| Node with a very large number of children | The solution should handle a large number of children without excessive memory allocation for intermediate results. |
| Children are in a specific order (sorted ascending or descending by value) | The order of children doesn't affect the traversal algorithm's correctness as long as the algorithm processes children consistently. |
| Integer overflow in node values (if applicable) | Consider the potential for integer overflow when processing node values, and use appropriate data types or checks to prevent it. |
| N-ary tree with a single path (all nodes have only one child) | The algorithm should correctly traverse this effectively linear structure. |
| Memory constraints for extremely large trees | For extremely large trees, consider processing in chunks or using disk-based data structures if memory becomes a limitation. |