Pascal's Triangle II
EasyGiven an integer rowIndex, return the rowIndexth (0-indexed) row of the Pascal's triangle.
In Pascal's triangle, each number is the sum of the two numbers directly above it as shown:
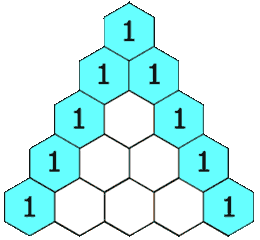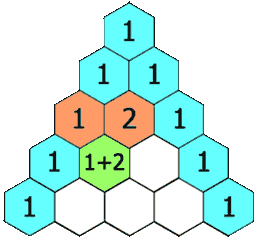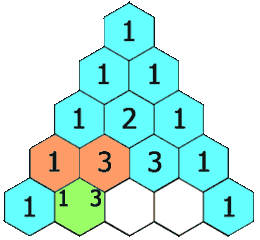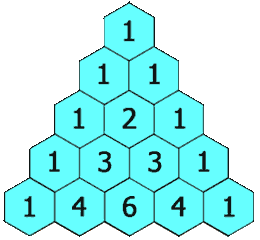
Example 1:
Input: rowIndex = 3 Output: [1,3,3,1]
Example 2:
Input: rowIndex = 0 Output: [1]
Example 3:
Input: rowIndex = 1 Output: [1,1]
Constraints:
0 <= rowIndex <= 33
Follow up: Could you optimize your algorithm to use only O(rowIndex) extra space?
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Is the `rowIndex` 0-indexed or 1-indexed?
- What is the maximum possible value for `rowIndex`? Is there an upper bound, and should I be concerned about integer overflow?
- Should I return an empty list if `rowIndex` is negative?
- Can I assume `rowIndex` will always be a valid integer?
- Can I use extra space, or should I try to optimize for space complexity as much as possible?
Brute Force Solution
Approach
The brute force approach to Pascal's Triangle II focuses on building the entire triangle row by row. We start from the top and compute each element based on the elements in the previous row, ultimately arriving at the desired row. We recalculate every value even if we've computed it before.
Here's how the algorithm would work step-by-step:
- Start by creating the first row of the triangle, which is just the number 1.
- Then, to build the next row, look at the row above it.
- For each number in the new row, calculate its value by adding the two numbers directly above it in the previous row.
- If a number is at the edge of the row, just consider the missing number as zero.
- Repeat this process, generating each row one at a time, until you reach the row that you're looking for.
- Once you've generated the row you wanted, that's your answer.
Code Implementation
def get_pascal_row_brute_force(row_index):
pascal_triangle = []
# The first row is always [1]
first_row = [1]
pascal_triangle.append(first_row)
for current_row_index in range(1, row_index + 1):
previous_row = pascal_triangle[current_row_index - 1]
current_row = []
# First element of each row is always 1
current_row.append(1)
# Calculate intermediate elements by summing the two elements above
for element_index in range(1, current_row_index):
# Sum the two numbers above in previous row
number_from_previous_row = previous_row[element_index - 1] + previous_row[element_index]
current_row.append(number_from_previous_row)
# Last element of each row is always 1
current_row.append(1)
pascal_triangle.append(current_row)
# Return the requested row of Pascal's Triangle
return pascal_triangle[row_index]Big(O) Analysis
Optimal Solution
Approach
To efficiently generate a specific row of Pascal's Triangle, we avoid calculating all the previous rows. Instead, we build the desired row directly, using the properties of Pascal's Triangle to update values in place.
Here's how the algorithm would work step-by-step:
- Imagine you have a list to store the row you want to create.
- Start by filling the list with ones. Every row in Pascal's Triangle begins and ends with one.
- Now, moving from left to right, update each number in the list based on the number before it. You can do this using a simple formula that relies on the previous number in the row.
- Repeat this process until you've reached the end of the row. This will correctly compute the next number in sequence using the previous ones.
- After updating the entire list, you'll have the numbers for the requested row of Pascal's Triangle.
Code Implementation
def get_row(row_index):
current_row = [1] * (row_index + 1)
# We calculate elements based on previous ones
for i in range(1, row_index + 1):
for j in range(i - 1, 0, -1):
# Update the current element based on its predecessor
current_row[j] = current_row[j] + current_row[j - 1]
return current_rowBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| rowIndex is negative | Return an empty list since Pascal's Triangle is not defined for negative rows. |
| rowIndex is 0 | Return a list containing only [1] since that's the first row of Pascal's Triangle. |
| rowIndex is a large positive integer that may cause integer overflow in calculating binomial coefficients. | Use long integer type or consider an alternative method (dynamic programming) to avoid potential integer overflow issues. |
| rowIndex is 1 | Return a list containing [1, 1] as the second row of Pascal's triangle. |
| rowIndex close to the maximum representable integer size | Ensure the algorithm gracefully handles maximum value limits by choosing suitable data types and preventing any overflow conditions during calculations. |
| Algorithm involves iterative calculation of elements, ensure each value is derived properly from the previous row | Use Dynamic Programming and only store one row at a time to avoid creating unnecessarily large data structures. |
| Space Complexity of generated triangle row | Optimize space by only storing and overwriting the last row. |
| Time complexity of calculating elements | Ensure generation of pascal's triangle is O(k^2) where k is rowIndex through use of optimal iterative approach. |