Pizza With 3n Slices
Hard
2 views
Topics:
ArraysDynamic Programming
There is a pizza with 3n slices of varying size, you and your friends will take slices of pizza as follows:
- You will pick any pizza slice.
- Your friend Alice will pick the next slice in the anti-clockwise direction of your pick.
- Your friend Bob will pick the next slice in the clockwise direction of your pick.
- Repeat until there are no more slices of pizzas.
Given an integer array slices that represent the sizes of the pizza slices in a clockwise direction, return the maximum possible sum of slice sizes that you can pick.
Example 1:
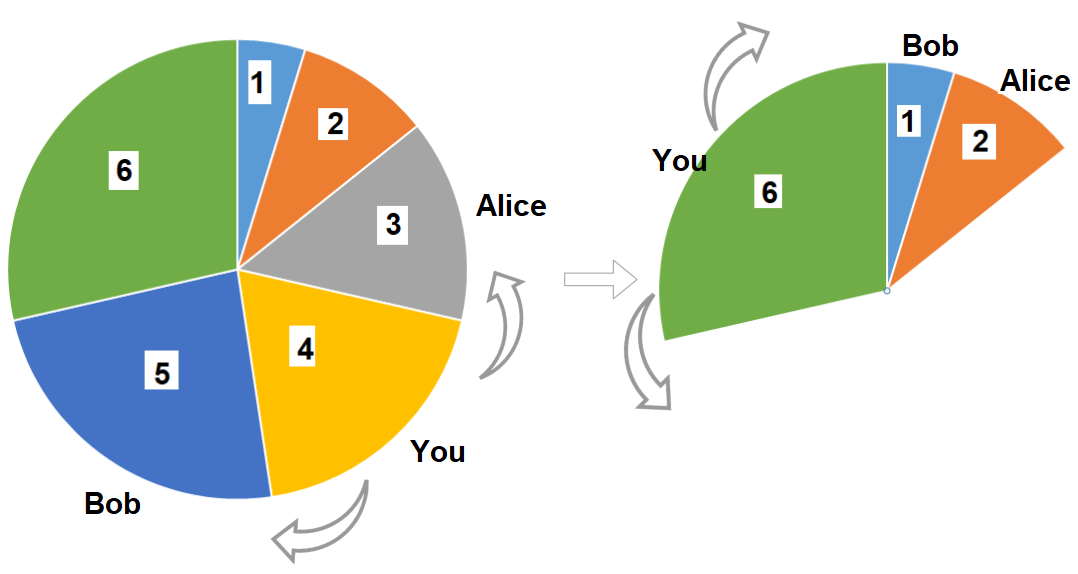
Input: slices = [1,2,3,4,5,6] Output: 10 Explanation: Pick pizza slice of size 4, Alice and Bob will pick slices with size 3 and 5 respectively. Then Pick slices with size 6, finally Alice and Bob will pick slice of size 2 and 1 respectively. Total = 4 + 6.
Example 2:
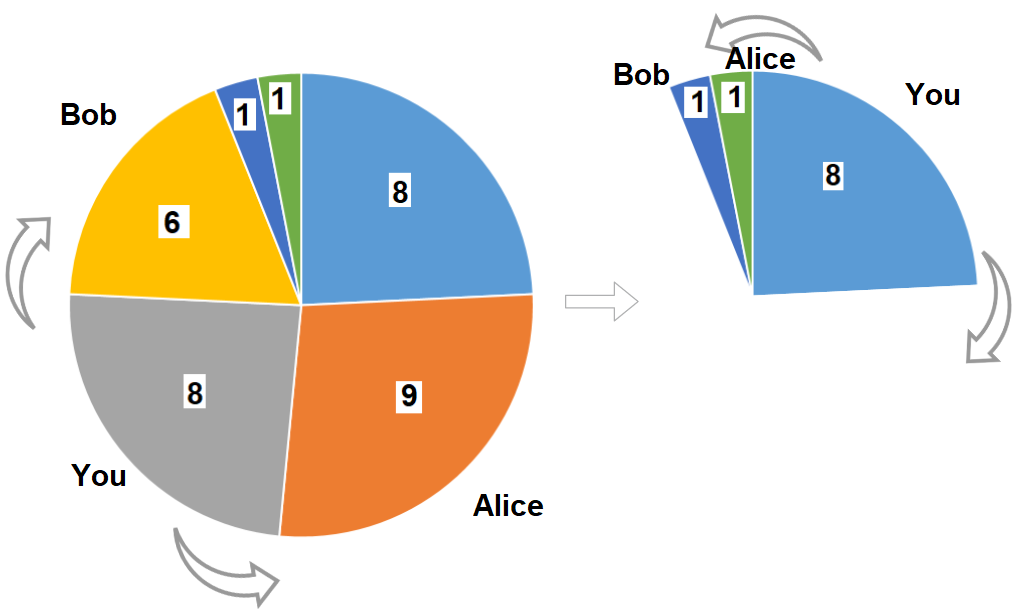
Input: slices = [8,9,8,6,1,1] Output: 16 Explanation: Pick pizza slice of size 8 in each turn. If you pick slice with size 9 your partners will pick slices of size 8.
Constraints:
3 * n == slices.length1 <= slices.length <= 5001 <= slices[i] <= 1000
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for the pizza slice sizes in the `slices` array? Can the slice sizes be negative or zero?
- Is `n` always a positive integer? What is the maximum possible value for `n`?
- If there's no way to pick `n` slices such that their sum is maximized and no two adjacent slices are picked, what should I return?
- Are there any constraints on the size of the `slices` array, besides that it will always have a length of `3n`?
- If multiple combinations of `n` slices result in the same maximum sum, is any one of those combinations acceptable as a valid solution?
Brute Force Solution
Approach
The brute force approach to the pizza problem involves trying every single combination of pizza slices we can take. We simply go through each possible subset of slices and see if that subset meets the criteria.
Here's how the algorithm would work step-by-step:
- Consider taking no slices at all and see if that works.
- Then, consider taking only the first slice and see if that's good.
- Next, consider taking only the second slice, then only the third slice, and so on, up to the last slice.
- Now, consider taking every possible pair of slices. For example, the first and second slice, the first and third slice, the second and fifth slice and so on.
- Continue this process, considering every possible group of three slices, four slices, and so on, all the way up to taking all the slices.
- For each group of slices you considered, check if taking those slices satisfies the rules: you can't take adjacent slices (directly next to each other), and you need to maximize the total value of the slices you take, without taking more than n slices.
- After checking every possible combination, find the combination that gives the highest total value and satisfies the rules. That's your best solution.
Code Implementation
def max_pizza_slices_brute_force(slices, number_of_friends):
number_of_slices = len(slices)
max_total_value = 0
# Iterate through all possible subsets of slices
for i in range(2 ** number_of_slices):
current_slices = []
total_value = 0
number_taken = 0
is_valid = True
# Build the current subset based on the bitmask i
for slice_index in range(number_of_slices):
if (i >> slice_index) & 1:
current_slices.append(slice_index)
# Check for adjacency and slice limit
for slice_index in range(len(current_slices)):
if slice_index > 0 and current_slices[slice_index] == current_slices[slice_index - 1] + 1:
is_valid = False
break
number_taken += 1
if number_taken > number_of_friends:
is_valid = False
#If the combination is valid, compute its value.
if is_valid:
for slice_index in current_slices:
total_value += slices[slice_index]
# Update the maximum value if needed
max_total_value = max(max_total_value, total_value)
return max_total_valueBig(O) Analysis
Time Complexity
O(2^n) – The provided brute force approach explores every possible subset of the input array of size n. This means considering all combinations, from taking no slices to taking all slices. Generating all subsets of a set with n elements requires 2^n operations, since each element can either be included or excluded from a subset. Therefore, the time complexity is exponential, specifically O(2^n), as it scales directly with the number of subsets.
Space Complexity
O(1) – The brute force approach described explores every possible subset of pizza slices. It does not explicitly mention creating and storing all these subsets in a separate data structure. The process iteratively examines combinations, possibly using a few variables to track the current subset's sum and count. No auxiliary data structures of size dependent on N (number of slices) are created or stored persistently. Therefore, the space complexity is constant, O(1).
Optimal Solution
Approach
The best way to solve this is to recognize it as a game of strategic picks. Instead of brute-forcing all slice combinations, we can intelligently choose slices that maximize our total and minimize waste based on a pattern.
Here's how the algorithm would work step-by-step:
- Think of the slices arranged in a circle.
- Consider two options: either you pick the first slice or you don't.
- If you pick the first slice, you can't pick the slices right next to it (the second and the last slice).
- If you don't pick the first slice, then you can pick from the rest of the slices without that restriction.
- For each of these two scenarios, pick the best slices you can, jumping over the slices that you can't pick because they're next to a slice you already chose.
- Compare the total number of slices you get in each scenario (picking the first slice vs. not picking the first slice) and select the one with the higher total.
- This approach avoids trying all possible combinations and quickly finds the best selection.
Code Implementation
def max_pizza_slices(slices):
number_of_slices = len(slices)
if number_of_slices == 0:
return 0
if number_of_slices == 1:
return slices[0]
def calculate_max_slices(available_slices):
number_of_available_slices = len(available_slices)
if number_of_available_slices == 0:
return 0
if number_of_available_slices == 1:
return available_slices[0]
dp_table = [0] * number_of_available_slices
dp_table[0] = available_slices[0]
dp_table[1] = max(available_slices[0], available_slices[1])
# Dynamic programming to determine max slices.
for i in range(2, number_of_available_slices):
dp_table[i] = max(dp_table[i - 1], dp_table[i - 2] + available_slices[i])
return dp_table[number_of_available_slices - 1]
# Consider picking the first slice
case_with_first_slice = calculate_max_slices(slices[1:number_of_slices - 1])
# Consider not picking the first slice
case_without_first_slice = calculate_max_slices(slices[0:number_of_slices])
# Select the case which returns a higher slice count
return max(case_with_first_slice, case_without_first_slice)Big(O) Analysis
Time Complexity
O(n log n) – The algorithm considers two scenarios: picking the first slice or not. In each scenario, we essentially select n slices (or rather, n/3 slices since we pick about a third of them) from a potentially modified array. The critical operation is finding the largest remaining slices in each subproblem. If we use a sorting or heap-based approach to find the largest slices, the dominant cost will be either sorting (O(n log n)) initially or repeatedly inserting into a heap (n log n) for n/3 extractions. Therefore, the overall time complexity is O(n log n).
Space Complexity
O(N) – The algorithm considers two scenarios: picking the first slice and not picking the first slice. For each scenario, it picks the best slices using a process that might implicitly require storing intermediate results or maintaining some state related to available slices. Since the number of slices that can be picked is related to the total number of slices, 3n (represented as N), the space used to track these intermediate results or available slices in each scenario scales linearly with N. This potentially results in temporary storage that is proportional to N, giving a space complexity of O(N).
Edge Cases
| Case | How to Handle |
|---|---|
| Empty `slices` array | Return 0 immediately, as no slices can be eaten. |
| `slices` array length is not divisible by 3 | This input is invalid per problem definition, so we should throw an IllegalArgumentException or return -1 to signal an error. |
| `slices` array contains only 3 elements. | The solution should correctly handle this minimal valid input by returning 1 if the first slice is chosen, 0 otherwise. |
| Large `slices` array causing potential memory issues. | Consider an iterative Dynamic Programming approach to minimize the space complexity to O(n). |
| All slices have the same size (e.g., all 1s) | The greedy approach might incorrectly maximize the slices, so a dynamic programming approach should be used for optimal selection. |
| Slice values are very large numbers, potentially leading to integer overflow during calculations. | Use `long` data type to store the values and intermediate calculations to avoid integer overflow. |
| Slice values are negative, which is physically impossible. | Throw an IllegalArgumentException or return -1 to signal an error as slice sizes cannot be negative. |
| Extreme skew in slice sizes (e.g., one slice is enormously bigger than the others). | Dynamic Programming correctly handles such cases as it explores all possible combinations to find the optimal solution |
Explore Interview QuestionsGoogle Interview QuestionsMeta Interview QuestionsAmazon Interview QuestionsApple Interview QuestionsNetflix Interview Questions
Explore Jobs By LevelEntry-Level Software Engineer JobsMid-Level Software Engineer JobsSenior Software Engineer JobsStaff Software Engineer Jobs
