Populating Next Right Pointers in Each Node

Medium

Amazon

1 view

Topics:

Trees

You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Example 1:

Input: root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]
Explanation: Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.

Example 2:

Input: root = []
Output: []

Constraints:

The number of nodes in the tree is in the range [0, 2¹² - 1].
-1000 <= Node.val <= 1000

Follow-up:

You may only use constant extra space.
The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem.

Populating Next Right Pointers in Each Node

Medium

Amazon

1 view

Topics:

Trees

You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.

Initially, all next pointers are set to NULL.

Example 1:

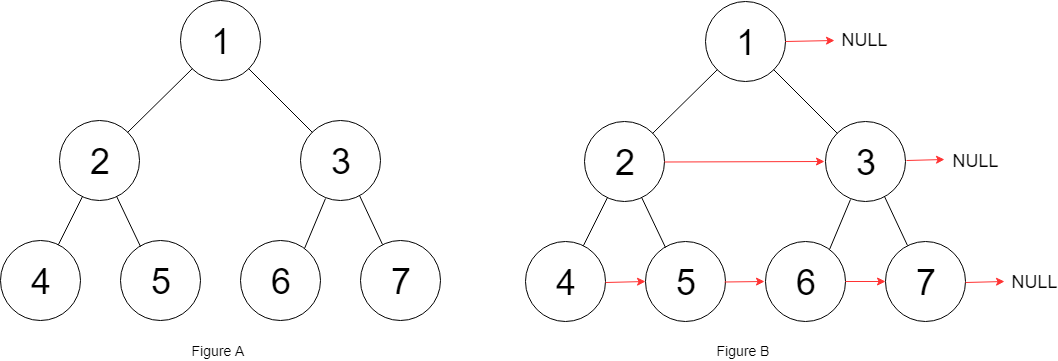
Input: root = [1,2,3,4,5,6,7]
Output: [1,#,2,3,#,4,5,6,7,#]
Explanation: Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with '#' signifying the end of each level.

Example 2:

Input: root = []
Output: []

Constraints:

The number of nodes in the tree is in the range [0, 2¹² - 1].
-1000 <= Node.val <= 1000

Follow-up:

You may only use constant extra space.
The recursive approach is fine. You may assume implicit stack space does not count as extra space for this problem.

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

Is the input a perfect binary tree, or is it a complete binary tree (or neither)?
What should the next pointer of the rightmost node on each level point to (null or some sentinel value)?
Are the node values unique, or can there be duplicate values in the tree?
Can I modify the given tree in-place, or do I need to create a new tree with the next pointers set?
What is the maximum depth of the tree I should expect?

Brute Force Solution

Approach

The brute force approach to connecting nodes on the same level is like manually checking every possible pair of nodes. We look at each node and then search through all other nodes on its level to find the one directly to its right. Once found, we connect them.

Here's how the algorithm would work step-by-step:

Start at the very top of the structure.
Go to the left most node on the second level.
Now, look at every other node on that same level to find the node that is immediately to its right.
Once you find the node to the right, make a connection (point the left node to the right node).
Move to the next node on the second level.
Repeat the process of finding the next right node and connecting them until you reach the end of the level.
Move down to the next level and do the same thing: find the right neighbor for each node and connect them.
Keep doing this for each level of the structure, going from left to right on each level, until you reach the bottom.

Code Implementation

class Node:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None
        self.next = None

def connect_nodes_brute_force(root):
    if not root:
        return root

    current_level_nodes = [root]

    while current_level_nodes:
        level_size = len(current_level_nodes)
        
        for i in range(level_size):
            current_node = current_level_nodes[i]
            # Finding right neighbor node
            for j in range(i + 1, level_size):
                right_neighbor = current_level_nodes[j]
                # Connect the node to its right neighbor
                current_node.next = right_neighbor
                break

        next_level_nodes = []
        for node in current_level_nodes:
            if node.left:
                next_level_nodes.append(node.left)
            if node.right:
                next_level_nodes.append(node.right)

        current_level_nodes = next_level_nodes
    return root

Big(O) Analysis

Time Complexity

O(n²) – The brute force approach, as described, iterates through each node and then searches for its next right pointer within the same level. In a complete binary tree, each level can contain up to n/2 nodes where n is the total number of nodes in the tree. For each node, we potentially compare it with all other nodes on its level. Therefore, the number of comparisons can grow quadratically with the input size n, approximating n * n/2 comparisons in total. This simplifies to O(n²).

Space Complexity

O(N) – The described brute force approach involves iterating through each level of the tree and, for each node, potentially searching through all other nodes on the same level to find its right neighbor. This search, in the worst-case scenario, could involve examining a significant portion of the level, implicitly requiring storage for the nodes on that level. Since in a complete binary tree, the last level can contain approximately N/2 nodes, the auxiliary space can grow linearly with N, where N is the total number of nodes in the tree. Therefore, the space complexity is O(N).

Optimal Solution

Approach

We want to connect each node in a perfect binary tree to its neighbor on the same level. The key idea is to use existing connections to efficiently traverse each level without extra memory, almost like an assembly line.

Here's how the algorithm would work step-by-step:

Start at the root of the tree, which has no neighbors to its right.
For each node, check if it has a left child. If not, we're done processing this level of the tree.
If there's a left child, connect that left child's 'next' pointer to its sibling, the right child.
If there's a node connected to this node on the same level (a 'next' neighbor), connect this right child's 'next' pointer to the 'next' neighbor's left child.
Move down to the next level by following the left child of the root. Now, repeat the process from the second step for this level of the tree.
Keep repeating the process level by level until you reach the bottom of the tree.

Code Implementation

class Node:
    def __init__(self, val=0, left=None, right=None, next=None):
        self.val = val
        self.left = left
        self.right = right
        self.next = next

def connect(root: Node) -> Node:
    if not root:
        return root

    leftmost_node = root

    while leftmost_node:
        current_node = leftmost_node
        while current_node:
            # Connect left child to right child.
            if current_node.left:
                current_node.left.next = current_node.right

                # Connect right child to next node's left child.
                if current_node.next:
                    current_node.right.next = current_node.next.left

            # Move to the next node on the same level.
            current_node = current_node.next

        # Move to the next level.
        # Ensures the process repeats for subsequent levels.
        leftmost_node = leftmost_node.left

    return root

Big(O) Analysis

Time Complexity

O(n) – The algorithm iterates through each node of the perfect binary tree exactly once. The outer loop implicitly traverses each level of the tree, and within each level, we connect each node to its next pointer, effectively visiting each node a single time. Since a perfect binary tree has n nodes, where n is the total number of nodes in the tree, the operations performed are directly proportional to n. Therefore, the time complexity is O(n).

Space Complexity

O(1) – The provided algorithm operates iteratively by traversing the tree level by level, utilizing existing 'next' pointers. It does not create any additional data structures like arrays, lists, or hash maps. The operations primarily involve pointer manipulation within the existing tree structure, with no auxiliary data storage proportional to the number of nodes (N). Therefore, the space complexity is constant.

Edge Cases

Case	How to Handle
Null root node	If the root is null, there is nothing to connect, so return null immediately.
Perfect binary tree with only one level (root only)	Root node's next pointer should remain null since it has no siblings.
Skewed binary tree (e.g., all nodes on left side)	Breadth-first or level-order traversal must correctly identify sibling at each level even in unbalanced cases.
Complete binary tree of maximum possible height (considering memory limits)	Ensure the algorithm uses memory efficiently and doesn't cause stack overflow (for recursive solutions) or exceed available memory (for queue-based solutions).
Binary tree where the connection between levels is the most complex	Level order or BFS solution accounts for all levels without special handling by using a queue.
Binary tree with identical node values	The algorithm should correctly link next pointers regardless of the node values.
Tree has only left children for certain nodes	The algorithm must correctly handle cases where right child doesn't exist, appropriately finding the next node or setting null.
Input is a malformed binary tree (cycles or disconnected subtrees - though unlikely)	Assume input is a valid binary tree as stated by prompt requirements.