Sum of Root To Leaf Binary Numbers
EasyYou are given the root of a binary tree where each node has a value 0 or 1. Each root-to-leaf path represents a binary number starting with the most significant bit.
- For example, if the path is
0 -> 1 -> 1 -> 0 -> 1, then this could represent01101in binary, which is13.
For all leaves in the tree, consider the numbers represented by the path from the root to that leaf. Return the sum of these numbers.
The test cases are generated so that the answer fits in a 32-bits integer.
Example 1:
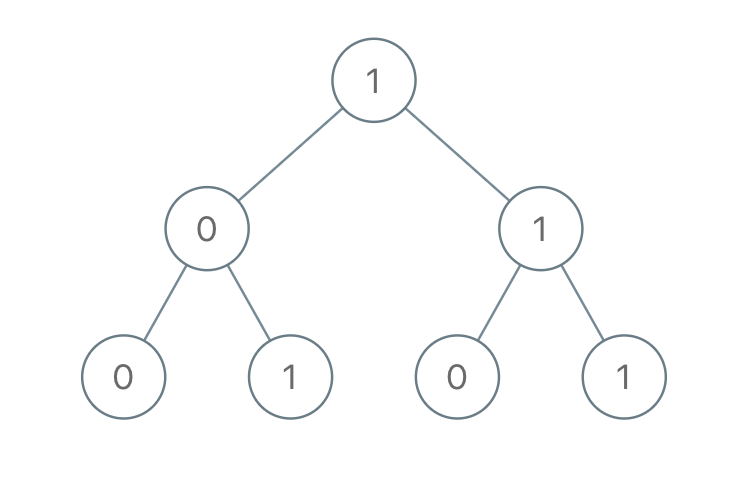
Input: root = [1,0,1,0,1,0,1] Output: 22 Explanation: (100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22
Example 2:
Input: root = [0] Output: 0
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. Node.valis0or1.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the maximum depth of the binary tree? This helps me understand potential stack overflow concerns with recursion.
- Can the nodes in the binary tree have values other than 0 and 1?
- Is it possible for the root to be null, representing an empty tree?
- Should I return 0 if the root is null?
- Are all root-to-leaf paths guaranteed to be valid binary numbers, or could there be leading zeros in the path?
Brute Force Solution
Approach
Imagine walking down every possible path from the top of a tree to each leaf. The brute force method explores all these paths, converting each path into a number, and then summing them up.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree (the root).
- Explore every possible path downwards, one step at a time.
- Each time you move down, remember the sequence of steps (0 or 1) you've taken so far to get there. Treat this sequence as a number.
- When you reach a leaf (the end of a path), calculate the number represented by that path from the root to that leaf.
- Add that number to a running total.
- Keep exploring all other paths until you've visited every leaf and added its corresponding number to the total.
- The final running total is the answer.
Code Implementation
def sum_root_to_leaf(root):
total_sum = 0
def dfs(node, current_number):
nonlocal total_sum
if not node:
return
# Update the current number based on the node value.
current_number = (current_number << 1) | node.val
# If it's a leaf node, add the current number to the total.
if not node.left and not node.right:
total_sum += current_number
return
dfs(node.left, current_number)
dfs(node.right, current_number)
dfs(root, 0)
return total_sumBig(O) Analysis
Optimal Solution
Approach
The key is to build the binary number representation as we walk down the tree, rather than waiting to reach the leaf node. This avoids storing or recomputing paths. We keep track of the current number and add the leaf value to form the complete binary number from root to leaf.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree (the root).
- As you go down to the next level (either left or right), take the current number and shift it to the left (multiply by 2) to make space for the new digit.
- Add the value of the current node (which will be either 0 or 1) to the shifted number. This is your new current number for that path.
- When you reach the end of a path (a leaf node), you've built a complete binary number from the root to that leaf. Add this number to a running total.
- Keep exploring all possible paths down the tree in this way.
- Once you've explored every path, the running total will be the sum of all the binary numbers represented by the paths from root to leaves.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def sum_root_to_leaf(root):
total_sum = 0
def calculate_sum(node, current_number):
nonlocal total_sum
if not node:
return
# Shift existing number to make space for new digit.
current_number = (current_number << 1) + node.val
# Leaf node: add the number to running total.
if not node.left and not node.right:
total_sum += current_number
return
# Explore the left and right subtrees.
calculate_sum(node.left, current_number)
calculate_sum(node.right, current_number)
calculate_sum(root, 0)
return total_sumBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty tree | Return 0 immediately, as there are no root-to-leaf paths. |
| Single node tree (root only) | Return the root's value directly as the only path sum. |
| Tree with all nodes having the value 0 | The sum will be 0, which the algorithm should handle correctly. |
| Tree with all nodes having the value 1, resulting in a very large binary number | Be mindful of potential integer overflow; use a larger data type if needed or perform modulo operations. |
| Highly unbalanced tree (skewed left or right) | The recursive call stack might become very deep, potentially leading to a stack overflow, so an iterative approach might be preferred for extreme cases. |
| Tree where all leaf nodes are at vastly different depths | The algorithm should still correctly calculate the binary number for each path, regardless of depth differences. |
| Integer overflow during binary number construction | Use modulo arithmetic with a large prime number to prevent integer overflow and keep the result within manageable bounds. |
| Tree with a very large number of nodes | The solution should scale linearly with the number of nodes, but memory usage might become a concern if each node consumes significant memory. |