Reverse Linked List II
MediumGiven the head of a singly linked list and two integers left and right where left <= right, reverse the nodes of the list from position left to position right, and return the reversed list.
Example 1:
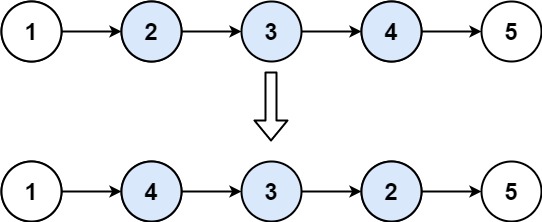
Input: head = [1,2,3,4,5], left = 2, right = 4 Output: [1,4,3,2,5]
Example 2:
Input: head = [5], left = 1, right = 1 Output: [5]
Constraints:
- The number of nodes in the list is
n. 1 <= n <= 500-500 <= Node.val <= 5001 <= left <= right <= n
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the valid ranges for `left` and `right`? Are they 1-indexed or 0-indexed?
- Can `left` be equal to `right`?
- Will `left` and `right` always be within the bounds of the linked list's length?
- Can the linked list be empty, or can `left` be less than 1?
- What should I return if the linked list is null or if `left` is greater than `right`?
Brute Force Solution
Approach
We want to reverse a portion of a linked list. The brute force way involves extracting the part we want to reverse, reversing it separately, and then putting everything back together in the correct order.
Here's how the algorithm would work step-by-step:
- First, find the starting and ending points of the section of the list that needs reversing.
- Next, grab that entire section and disconnect it from the original list.
- Now, reverse the order of the nodes within that extracted section.
- Finally, re-attach the reversed section back into the original list, making sure everything is linked up correctly before and after the reversed part.
Code Implementation
def reverse_linked_list_between(head, left, right):
if not head or left == right:
return head
dummy_node = ListNode(0)
dummy_node.next = head
previous_node = dummy_node
# Find the node just before the start of reversal
for _ in range(left - 1):
previous_node = previous_node.next
current_node = previous_node.next
# Extract the sublist to be reversed
nodes_to_reverse = []
for _ in range(right - left + 1):
nodes_to_reverse.append(current_node)
current_node = current_node.next
# Disconnect the sublist from original list
previous_node.next = current_node
# Reverse the sublist
nodes_to_reverse.reverse()
# Re-attach the reversed sublist
previous_node.next = nodes_to_reverse[0]
for i in range(len(nodes_to_reverse) - 1):
nodes_to_reverse[i].next = nodes_to_reverse[i + 1]
# Link the end of reversed list to rest of original
nodes_to_reverse[-1].next = current_node
return dummy_node.nextBig(O) Analysis
Optimal Solution
Approach
We're given a chain of connected items, and need to flip a section of it in place. The trick is to carefully disconnect and reconnect parts of the chain to reverse only the specified section, leaving the rest of the chain intact.
Here's how the algorithm would work step-by-step:
- First, locate the item right before the section you want to reverse. Remember this item, as it will be the new connection point to the reversed section.
- Also, find the very first item in the section you want to reverse. We'll call this the starting point of our reversal.
- Now, go through the section you want to reverse, one item at a time. With each item, flip its connection to point to the previous item. This effectively reverses the direction of the connections within that section.
- As you reverse, keep track of the last item in the reversed section. This will become the new tail of the reversed portion.
- Once the entire section is reversed, connect the item you remembered before the section to the new tail of the reversed section.
- Then, connect the starting point of the original section (which is now the end of the reversed part) to the item that followed the original reversed section.
- If the reversal starts from the very beginning of the chain, remember to update the chain's beginning to the new head of the reversed portion.
Code Implementation
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
def reverse_linked_list_ii(head, left, right):
if not head or left == right:
return head
dummy_node = ListNode(0)
dummy_node.next = head
previous_node = dummy_node
# Find the node before the sublist to be reversed.
for _ in range(left - 1):
previous_node = previous_node.next
current_node = previous_node.next
#Iteratively reverse the desired portion of the linked list.
for _ in range(right - left):
next_node = current_node.next
current_node.next = next_node.next
next_node.next = previous_node.next
previous_node.next = next_node
#If reversing from the head, return the new head.
if left == 1:
return dummy_node.next
return headBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty linked list (head is null) | Return null immediately since there is nothing to reverse. |
| m equals n (no reversal needed) | Return the original head, as no reversal is required. |
| m equals 1 (reversal starts from the head) | The head pointer must be updated after the reversal. |
| n equals the length of the list (reversal goes to the end) | The tail of the reversed portion should point to null if n is the last element. |
| Invalid input: m > n | Throw an IllegalArgumentException or return null to indicate an invalid input. |
| m or n are out of bounds (less than 1 or greater than list length) | Throw an IllegalArgumentException or return null to indicate an invalid input. |
| List with only one element | Return the original head since there's nothing to reverse. |
| Large list (potential memory/performance issues) | Iterative approach is preferred over recursive approach to avoid stack overflow and ensure efficiency for larger lists. |