Word Search
MediumGiven an m x n grid of characters board and a string word, return true if word exists in the grid.
The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.
Example 1:
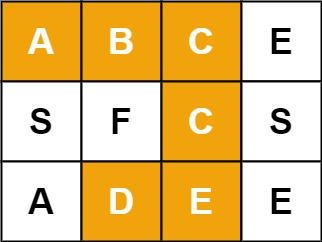
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED" Output: true
Example 2:
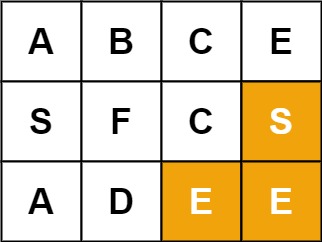
Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "SEE" Output: true
Example 3:

Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCB" Output: false
Constraints:
m == board.lengthn = board[i].length1 <= m, n <= 61 <= word.length <= 15boardandwordconsists of only lowercase and uppercase English letters.
Follow up: Could you use search pruning to make your solution faster with a larger board?
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the board, and what is the maximum length of the word? This will help me understand the scale of the input.
- Can the board contain characters other than letters? Are the letters in the word guaranteed to be present in the board?
- Is the word case-sensitive? Should I treat 'A' and 'a' as the same letter or as different letters?
- If the word can be found multiple times in the board, should I return true after finding the first instance, or do I need to find all possible instances?
- Is the board guaranteed to be rectangular (i.e., all rows have the same number of columns)? What should I return if either the board or the word is empty or null?
Brute Force Solution
Approach
Imagine searching for a word hidden in a grid of letters. The brute force method involves checking every possible path through the grid to see if it spells out the word. We'll explore all potential starting points and directions until we find the word or exhaust all possibilities.
Here's how the algorithm would work step-by-step:
- Begin by picking any letter in the grid as a potential starting point for the word.
- From that starting letter, check all the letters next to it (up, down, left, right) to see if any of them match the second letter of the word we are searching for.
- If we find a matching second letter, we then check all the letters next to that second letter (again, up, down, left, right) to see if they match the third letter of our word. It's important to remember we can't revisit the same letter we already used on this particular path.
- Continue this process, extending the path, until we either find the entire word or reach a dead end (no matching letters are found next to the current letter).
- If we reach a dead end, we backtrack and try a different path. If we can't find the word using this starting letter, we then select a different letter in the grid as the starting point and repeat the entire process.
- We continue doing this for every single letter in the grid, exploring all possible paths until the word is found or all paths are exhausted.
Code Implementation
def word_search(board, word):
number_of_rows = len(board)
number_of_columns = len(board[0])
def depth_first_search(row, column, word_index, visited):
if word_index == len(word):
return True
if (row < 0 or row >= number_of_rows or
column < 0 or column >= number_of_columns or
board[row][column] != word[word_index] or
(row, column) in visited):
return False
# Mark the current cell as visited to avoid revisiting.
visited.add((row, column))
found = (depth_first_search(row + 1, column, word_index + 1, visited.copy()) or
depth_first_search(row - 1, column, word_index + 1, visited.copy()) or
depth_first_search(row, column + 1, word_index + 1, visited.copy()) or
depth_first_search(row, column - 1, word_index + 1, visited.copy()))
return found
# Iterate through each cell in the board as a starting point.
for row in range(number_of_rows):
for column in range(number_of_columns):
# Initiate DFS from the current cell if it matches
# the first character of the target word
if board[row][column] == word[0]:
if depth_first_search(row, column, 0, set()):
return True
# No path found for the specified word
return FalseBig(O) Analysis
Optimal Solution
Approach
This problem asks us to find a word in a grid of letters. The optimal strategy involves systematically exploring possible paths in the grid, checking if the letters along the path match the letters of the word we're searching for. We avoid re-exploring paths we've already tried.
Here's how the algorithm would work step-by-step:
- Start by looking at each letter in the grid as a potential starting point for the word.
- If a letter matches the first letter of the word, explore the neighboring letters (up, down, left, and right) to see if they match the second letter of the word.
- Continue exploring adjacent letters, building the path one letter at a time, making sure you only move to letters that match the next letter in the word.
- To avoid getting stuck in cycles, keep track of which letters in the grid you've already visited along a particular path, and don't revisit them.
- If you find a path that spells out the entire word, you've found a match and can stop searching.
- If you explore all possible paths from all starting points and don't find the word, it doesn't exist in the grid.
Code Implementation
def word_search(board, word):
number_of_rows = len(board)
number_of_columns = len(board[0])
def depth_first_search(row, column, word_index, visited_cells):
if word_index == len(word):
return True
if row < 0 or row >= number_of_rows or column < 0 or column >= number_of_columns or (row, column) in visited_cells or board[row][column] != word[word_index]:
return False
# Mark current cell as visited to prevent cycles
visited_cells.add((row, column))
found = (depth_first_search(row + 1, column, word_index + 1, visited_cells.copy()) or
depth_first_search(row - 1, column, word_index + 1, visited_cells.copy()) or
depth_first_search(row, column + 1, word_index + 1, visited_cells.copy()) or
depth_first_search(row, column - 1, word_index + 1, visited_cells.copy()))
return found
# Iterate through each cell on the board
for row in range(number_of_rows):
for column in range(number_of_columns):
# Initiate DFS search from the matching cell
if board[row][column] == word[0]:
if depth_first_search(row, column, 0, set()):
return True
# If word not found, return false
return FalseBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| board is null or empty | Return false immediately as no search is possible. |
| word is null or empty | Return true immediately as an empty word is always found. |
| board is smaller than word | Return false immediately, word cannot be found. |
| Word longer than the total letters on the board | Return false since the word cannot possibly exist on the board. |
| Word contains characters not present in the board | The DFS search will not find a starting point and thus will return false. |
| Board and word contain only one character. | The initial check and DFS will compare the characters and return true or false. |
| Word appears multiple times in the board (overlapping paths not allowed). | The used character check prevents revisiting cells within a single search, ensuring each character in the board is used at most once per search attempt. |
| Large board and long word causing potential stack overflow in recursive DFS. | The solution should consider iterative DFS with an explicit stack to handle extremely large inputs without stack overflow. |