Binary Tree Level Order Traversal II
MediumGiven the root of a binary tree, return the bottom-up level order traversal of its nodes' values. (i.e., from left to right, level by level from leaf to root).
Example 1:
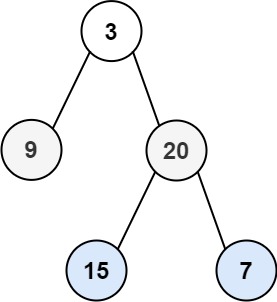
Input: root = [3,9,20,null,null,15,7] Output: [[15,7],[9,20],[3]]
Example 2:
Input: root = [1] Output: [[1]]
Example 3:
Input: root = [] Output: []
Constraints:
- The number of nodes in the tree is in the range
[0, 2000]. -1000 <= Node.val <= 1000
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can the binary tree be empty? What should I return in that case?
- What is the range of values that the nodes in the binary tree can have?
- Should I return an empty list if the tree is empty, or is null an acceptable return value?
- Is the expected output a list of lists of integers, and is the order within each level (inner list) significant?
- Are we dealing with a complete, balanced, or potentially skewed binary tree?
Brute Force Solution
Approach
We want to visit every level of the tree and collect the nodes, but starting from the bottom. The brute force way is to visit each node and figure out what level it is on, then sort the nodes by level in reverse order.
Here's how the algorithm would work step-by-step:
- Go through the entire tree, looking at each node one at a time.
- For each node you find, figure out how far away it is from the root of the tree. This tells you what level it's on.
- Now that you know what level each node is on, group all the nodes together that are on the same level.
- Arrange these groups so the bottom level is first, then the level above it, and so on until you get to the root level at the end.
- The result is the tree level order traversal, but with the levels in reverse order.
Code Implementation
def binary_tree_level_order_traversal_ii(root):
if not root:
return []
node_levels = []
def get_level(node, current_level):
if not node:
return
node_levels.append((node, current_level))
get_level(node.left, current_level + 1)
get_level(node.right, current_level + 1)
# Traverse the tree to determine the level of each node.
get_level(root, 0)
level_map = {}
for node, level in node_levels:
if level not in level_map:
level_map[level] = []
level_map[level].append(node.val)
# We must sort levels to guarantee reverse level order.
sorted_levels = sorted(level_map.keys(), reverse=True)
result = []
# Build result based on levels.
for level in sorted_levels:
result.append(level_map[level])
return result
Big(O) Analysis
Optimal Solution
Approach
We need to visit every level of the tree and organize the nodes at each level. The trick is to process the levels from top to bottom, but then reverse the order of the final result to get the bottom levels first. This lets us build the levels in the natural way, but present them in the requested order.
Here's how the algorithm would work step-by-step:
- Use a method that explores the tree level by level from the top downwards. This is like reading a book, line by line.
- At each level, collect all the node values into a temporary collection.
- After you finish processing all the levels, you will have a collection of collections, where each internal collection represents a level's nodes.
- Now, reverse the order of the levels. That is, flip the collection so the last level becomes the first, and the first level becomes the last.
- The result is the levels of the tree, ordered from the bottom to the top, as desired.
Code Implementation
from collections import deque
def binaryTreeLevelOrderTraversal2(root):
if not root:
return []
levels = []
queue = deque([root])
while queue:
level_size = len(queue)
current_level_values = []
# Process all nodes at the current level
for _ in range(level_size):
node = queue.popleft()
current_level_values.append(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
levels.append(current_level_values)
# Reverse the order of levels
levels.reverse()
return levelsBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null root | Return an empty list immediately since there is no tree to traverse. |
| Single node tree | Return a list containing a list with the single node's value. |
| Perfectly balanced tree | The algorithm should process this efficiently, demonstrating optimal performance. |
| Completely unbalanced (skewed) tree (left or right) | The algorithm should handle the varying level sizes gracefully and depth of tree without stack overflow. |
| Tree with duplicate values | The level order traversal should correctly include all duplicate values at their respective levels. |
| Very large tree (memory constraints) | Consider space complexity; for extremely large trees, using an iterative approach with a queue might be preferred to minimize memory usage compared to recursive approaches which might cause stackoverflow. |
| Tree with negative values | The algorithm should correctly process negative values as valid node data without any type overflow. |
| Integer overflow during tree processing if node values are very large | Ensure operations on node values (e.g., summing for calculations) are done within integer limits by selecting appropriate data structures. |