Rotate Image
MediumYou are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).
You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.
Example 1:
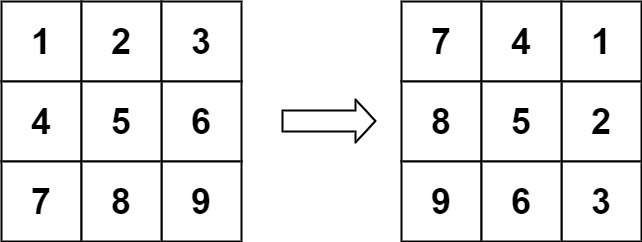
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]] Output: [[7,4,1],[8,5,2],[9,6,3]]
Example 2:
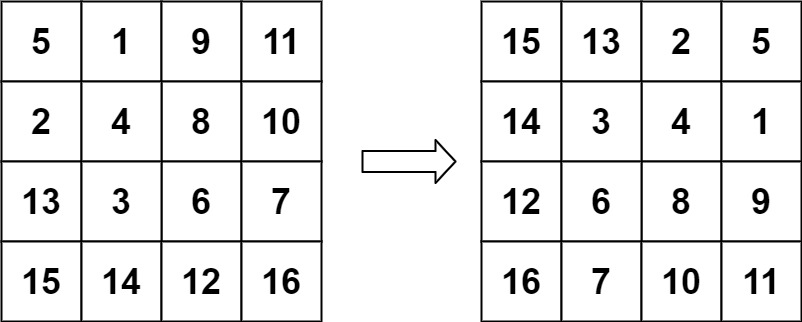
Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
Constraints:
n == matrix.length == matrix[i].length1 <= n <= 20-1000 <= matrix[i][j] <= 1000
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Is the input matrix guaranteed to be a square matrix (N x N)? What is the maximum size of N?
- Can the matrix contain negative numbers, zero, or floating-point numbers, or are all elements guaranteed to be positive integers?
- Should I handle the case where the input matrix is null or empty?
- Is it acceptable to use extra space proportional to the size of the matrix, or must the rotation be done strictly in-place with O(1) extra space?
- If the input is a 1x1 matrix, should it be considered already rotated and returned without modification?
Brute Force Solution
Approach
Rotating an image the hard way involves creating a new, empty image. We then systematically copy each pixel from the original image to its new, rotated position in the new image.
Here's how the algorithm would work step-by-step:
- Create a completely new, blank image with the same size as the original image.
- Look at the very first pixel in the original image.
- Figure out where that specific pixel *should* go in the rotated image.
- Copy the color of that pixel from the original image to its calculated spot in the new, rotated image.
- Repeat steps 2-4 for *every* pixel in the original image, one by one, until you've copied them all to their correct, rotated locations in the new image.
- Now the new image contains the rotated version of the original.
Code Implementation
def rotate_image_brute_force(image):
matrix_size = len(image)
# Create a new matrix to hold the rotated image
rotated_image = [[0] * matrix_size for _ in range(matrix_size)]
for row in range(matrix_size):
for col in range(matrix_size):
# Calculate the new row and column indices after rotation
new_row = col
new_col = matrix_size - 1 - row
# Assign the pixel to the new location
rotated_image[new_row][new_col] = image[row][col]
return rotated_imageBig(O) Analysis
Optimal Solution
Approach
To rotate an image represented as a grid, we don't actually swap individual pixels one-by-one. Instead, we perform the rotation in two steps. These two transformations, when combined, achieve the desired 90-degree clockwise rotation efficiently.
Here's how the algorithm would work step-by-step:
- First, imagine flipping the image across its main diagonal – the one going from the top-left to the bottom-right corner. This is like creating a mirror image along that line, swapping elements symmetrically.
- Next, flip the image horizontally, swapping the first column with the last, the second with the second-to-last, and so on. This essentially mirrors the image left to right.
- By performing these two flips in order, we achieve a 90-degree clockwise rotation of the original image.
Code Implementation
def rotate_image(matrix):
matrix_size = len(matrix)
# Transpose the matrix, flipping across the main diagonal.
for i in range(matrix_size):
for j in range(i, matrix_size):
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
# Reverse each row to complete the 90-degree clockwise rotation.
# This achieves horizontal reflection after transposition.
for row in matrix:
row.reverse()
Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or Empty Matrix | Check for null or empty matrix at the beginning and return immediately as there is nothing to rotate. |
| 1x1 Matrix | No rotation is needed for a 1x1 matrix; return the matrix unchanged. |
| 2x2 Matrix | The algorithm should correctly rotate a minimal 2x2 matrix, verifying the base rotation logic. |
| Non-square matrix | The problem statement assumes a square matrix; if non-square, either throw an IllegalArgumentException or define alternative rotation behavior and implement that. |
| Matrix with large integer values (close to Integer.MAX_VALUE or Integer.MIN_VALUE) | The in-place swap operation might cause integer overflow if values are close to Integer.MAX_VALUE or Integer.MIN_VALUE, consider handling this scenario or document its possibility. |
| Large Matrix (e.g., 1000x1000) | Ensure the solution does not cause a stack overflow due to excessive recursion (if using recursion) and scales linearly with the number of elements, as the rotation has O(n^2) time complexity. |
| Matrix with all identical values | The algorithm should still function correctly even if all elements are the same. |
| Matrix containing zeros and negative numbers | The swapping algorithm must correctly handle zeros and negative numbers within the matrix. |