Symmetric Tree
EasyGiven the root of a binary tree, check whether it is a mirror of itself (i.e., symmetric around its center).
Example 1:
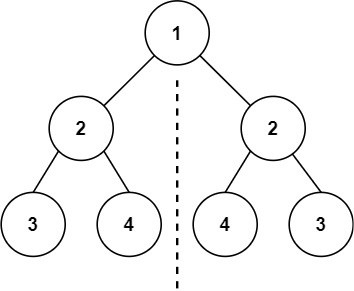
Input: root = [1,2,2,3,4,4,3] Output: true
Example 2:
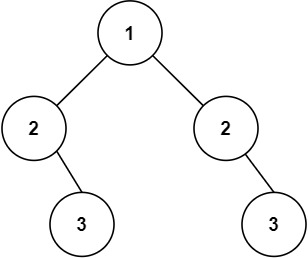
Input: root = [1,2,2,null,3,null,3] Output: false
Constraints:
- The number of nodes in the tree is in the range
[1, 1000]. -100 <= Node.val <= 100
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values that the nodes in the binary tree can hold?
- Can the tree be empty (i.e., root is null)? If so, should an empty tree be considered symmetric?
- By symmetric, do you mean structurally identical with reversed values at corresponding nodes?
- Are there any specific memory constraints I should be aware of, given the potential size of the tree?
- Is the input a valid binary tree, or do I need to handle cases where the tree structure is somehow invalid?
Brute Force Solution
Approach
To check if a tree is symmetric, we're essentially seeing if the left and right halves mirror each other. The brute force way is to painstakingly examine every single possibility for how the tree's structure could be, focusing on comparing the left and right sides at each step.
Here's how the algorithm would work step-by-step:
- First, look at the entire tree. If both sides are empty, it's symmetric. If only one side is empty, it's not.
- If both sides have something, compare their values. If they're different, the tree isn't symmetric.
- If they're the same, look at the left 'child' of the left side and the right 'child' of the right side. Compare those. If they're different, the tree isn't symmetric.
- Then, look at the right 'child' of the left side and the left 'child' of the right side. Compare those. If they're different, the tree isn't symmetric.
- Keep repeating these comparisons level by level. Each time, make sure you're comparing the left side's mirror to the right side. If you find even one mismatch at any point, the whole tree is not symmetric.
- If you've gone through every possible comparison and haven't found any mismatches, then the tree is symmetric.
Code Implementation
def is_symmetric(root_node):
# Empty tree is defined as symmetric
if not root_node:
return True
return are_mirrored(root_node.left, root_node.right)
def are_mirrored(left_tree, right_tree):
if not left_tree and not right_tree:
return True
if not left_tree or not right_tree:
return False
# Must have equal values to be symmetric
if left_tree.val != right_tree.val:
return False
# Recursive check of inner and outer nodes
return are_mirrored(left_tree.left, right_tree.right) and\
are_mirrored(left_tree.right, right_tree.left)
Big(O) Analysis
Optimal Solution
Approach
The key idea is to check if the tree is symmetric by comparing the structure of the left and right subtrees. We consider the tree symmetric if the left subtree is a mirror image of the right subtree. To efficiently determine symmetry, we use a technique to compare corresponding nodes of the left and right subtrees simultaneously.
Here's how the algorithm would work step-by-step:
- Imagine folding the tree in half along its root. Now, we want to see if the two halves match perfectly.
- Start by comparing the root's left child with the root's right child.
- Check if both children exist. If they both exist, compare their values. If the values are different, the tree isn't symmetric.
- If the values are the same, go deeper. Compare the left child's left child with the right child's right child, and the left child's right child with the right child's left child.
- Continue this process, always comparing the 'outer' nodes with each other and the 'inner' nodes with each other as we go down the tree.
- If, at any point, one side has a node and the other side doesn't, or the values of the corresponding nodes don't match, the tree isn't symmetric.
- If we reach the end without finding any mismatches, the tree is symmetric.
Code Implementation
class TreeNode:
def __init__(self, value=0, left=None, right=None):
self.value = value
self.left = left
self.right = right
def is_symmetric(root: TreeNode) -> bool:
def is_mirror(left_node: TreeNode, right_node: TreeNode) -> bool:
# If both are None, they are symmetric.
if not left_node and not right_node:
return True
# If only one is None, they are not symmetric.
if not left_node or not right_node:
return False
# If values are different, not symmetric
if left_node.value != right_node.value:
return False
# Recursively check the inner and outer nodes
return is_mirror(left_node.left, right_node.right) and \
is_mirror(left_node.right, right_node.left)
# Handle empty tree case, an empty tree is considered symmetric
if not root:
return True
# Start comparison with the root's left and right children
return is_mirror(root.left, root.right)
Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty Tree (null root) | The tree is considered symmetric, so return true. |
| Single Node Tree | The tree is considered symmetric because the left and right subtrees are effectively empty/null, so return true. |
| Tree with root, only left child | The left and right subtrees are not mirror images, so return false. |
| Tree with root, only right child | The left and right subtrees are not mirror images, so return false. |
| Completely Symmetric Tree with many nodes | The algorithm should correctly identify it as symmetric without stack overflow (recursion) or excessive runtime (iteration). |
| Asymmetric Tree | The algorithm should correctly identify it as asymmetric by finding a mismatch in structure or values. |
| Tree with identical values at different levels but different structure | The algorithm must compare both the values AND structure to ensure symmetry and return false if they are not identical mirrors. |
| Skewed Tree (all nodes on one side) | The algorithm should correctly identify this as asymmetric since the mirrored side is effectively missing. |