Largest Rectangle in Histogram
HardGiven an array of integers heights representing the histogram's bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.
Example 1:
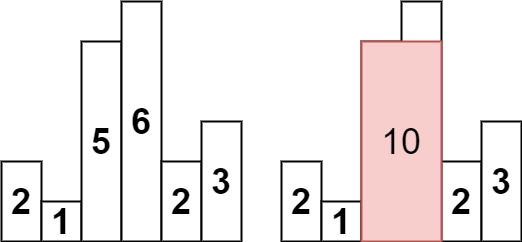
Input: heights = [2,1,5,6,2,3] Output: 10 Explanation: The above is a histogram where width of each bar is 1. The largest rectangle is shown in the red area, which has an area = 10 units.
Example 2:
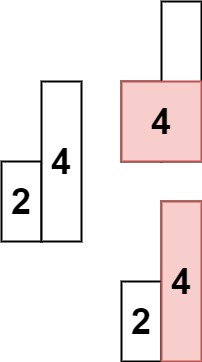
Input: heights = [2,4] Output: 4
Constraints:
1 <= heights.length <= 1050 <= heights[i] <= 104
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the maximum size of the `heights` array, and what is the range of values for each height in the array?
- Can the `heights` array be empty, or can any of the heights be zero?
- If there are multiple rectangles with the same largest area, is it sufficient to return any one of those areas?
- Are the heights guaranteed to be non-negative integers?
- Is there an explicit constraint or expectation on memory usage?
Brute Force Solution
Approach
The brute force strategy for the histogram problem is all about trying everything. We will look at every possible rectangle we can form within the histogram and calculate its area. Finally, we find the rectangle with the biggest area.
Here's how the algorithm would work step-by-step:
- For every possible starting point in the histogram, consider it as the left edge of a rectangle.
- Then, for each left edge, expand the rectangle to the right, one bar at a time.
- As we expand the rectangle to the right, find the shortest bar encountered so far. This shortest bar will be the height of our current rectangle.
- Calculate the area of this rectangle by multiplying the shortest bar height by the width of the rectangle (the number of bars included).
- Compare the calculated area with the largest area we've seen so far. If the current area is bigger, update the largest area.
- Repeat this process for all possible starting points and expansions to the right. This way, we've checked every possible rectangular area.
- After considering all possible rectangles, the largest area found is the answer.
Code Implementation
def largest_rectangle_in_histogram_brute_force(heights):
largest_area = 0
number_of_heights = len(heights)
for left_edge in range(number_of_heights):
# Consider each bar as the potential left edge
for right_edge in range(left_edge, number_of_heights):
minimum_height = float('inf')
for index in range(left_edge, right_edge + 1):
minimum_height = min(minimum_height, heights[index])
# Find the smallest height between left and right edges
width = right_edge - left_edge + 1
current_area = minimum_height * width
# Expand the rectangle to the right and calculate area
largest_area = max(largest_area, current_area)
# Update largest area if necessary
return largest_areaBig(O) Analysis
Optimal Solution
Approach
The most efficient way to solve this is to keep track of the potential for building tall rectangles as you go. We use a special tool to help us remember where we are in the histogram and efficiently find the best rectangle.
Here's how the algorithm would work step-by-step:
- Imagine a stack of blocks where each block's height represents a bar in the histogram.
- Go through the histogram bar by bar. If the current bar is taller than the last block on our stack, add it to the stack.
- If the current bar is shorter than the last block, it means we need to calculate the area of the tallest rectangle we can make using blocks from the stack.
- Take blocks off the stack one by one until the last block is shorter than the current bar.
- For each block you take off, figure out the biggest rectangle you can make using that block as the shortest side. The width of the rectangle is how far you are into the original set of bars, minus the blocks that are still remaining on the stack.
- After looking at all the bars, do one final calculation to remove any remaining blocks from the stack. This ensures we have calculated all possible rectangles.
- Keep track of the largest rectangle area you find. At the end, this will be your answer.
Code Implementation
def largestRectangleArea(heights):
stack = []
max_area = 0
index = 0
while index < len(heights):
if not stack or heights[index] > heights[stack[-1]]:
stack.append(index)
index += 1
else:
# Current height is less so calculate area.
top_of_stack = stack.pop()
area = (heights[top_of_stack] *
((index - stack[-1] - 1) if stack else index))
max_area = max(max_area, area)
# Calculate the area for the remaining bars.
while stack:
top_of_stack = stack.pop()
area = (heights[top_of_stack] *
((index - stack[-1] - 1) if stack else index))
# Store the largest area.
max_area = max(max_area, area)
return max_areaBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty input array | Return 0 as there are no bars to form a rectangle. |
| Array with a single element | Return the value of the single element as the largest area is the height itself. |
| Array with all identical values | The largest rectangle area is the height multiplied by the width (array length). |
| Array with heights in strictly increasing order | The algorithm should correctly calculate decreasing areas from right to left. |
| Array with heights in strictly decreasing order | The algorithm should correctly calculate increasing areas from left to right. |
| Large input array (performance consideration) | The stack-based approach handles large arrays efficiently with O(n) time complexity. |
| Heights with very large values that can lead to integer overflow when calculating area | Use long data type for calculating area to prevent overflow. |
| Array containing zero values | Zero values should be treated as valid heights, potentially limiting the area of rectangles. |