Minimum Operations to Write the Letter Y on a Grid

Medium

Capital One

3 views

Topics:

Arrays

You are given a 0-indexed n x n grid where n is odd, and grid[r][c] is 0, 1, or 2.

We say that a cell belongs to the Letter Y if it belongs to one of the following:

The diagonal starting at the top-left cell and ending at the center cell of the grid.
The diagonal starting at the top-right cell and ending at the center cell of the grid.
The vertical line starting at the center cell and ending at the bottom border of the grid.

The Letter Y is written on the grid if and only if:

All values at cells belonging to the Y are equal.
All values at cells not belonging to the Y are equal.
The values at cells belonging to the Y are different from the values at cells not belonging to the Y.

Return the minimum number of operations needed to write the letter Y on the grid given that in one operation you can change the value at any cell to 0, 1, or 2.

Example 1:

Input: grid = [[1,2,2],[1,1,0],[0,1,0]]
Output: 3
Explanation: We can write Y on the grid by applying the changes highlighted in blue in the image above. After the operations, all cells that belong to Y, denoted in bold, have the same value of 1 while those that do not belong to Y are equal to 0.
It can be shown that 3 is the minimum number of operations needed to write Y on the grid.

Example 2:

Input: grid = [[0,1,0,1,0],[2,1,0,1,2],[2,2,2,0,1],[2,2,2,2,2],[2,1,2,2,2]]
Output: 12
Explanation: We can write Y on the grid by applying the changes highlighted in blue in the image above. After the operations, all cells that belong to Y, denoted in bold, have the same value of 0 while those that do not belong to Y are equal to 2. 
It can be shown that 12 is the minimum number of operations needed to write Y on the grid.

Constraints:

3 <= n <= 49
n == grid.length == grid[i].length
0 <= grid[i][j] <= 2
n is odd.

Minimum Operations to Write the Letter Y on a Grid

Medium

Capital One

3 views

Topics:

Arrays

You are given a 0-indexed n x n grid where n is odd, and grid[r][c] is 0, 1, or 2.

We say that a cell belongs to the Letter Y if it belongs to one of the following:

The diagonal starting at the top-left cell and ending at the center cell of the grid.
The diagonal starting at the top-right cell and ending at the center cell of the grid.
The vertical line starting at the center cell and ending at the bottom border of the grid.

The Letter Y is written on the grid if and only if:

All values at cells belonging to the Y are equal.
All values at cells not belonging to the Y are equal.
The values at cells belonging to the Y are different from the values at cells not belonging to the Y.

Return the minimum number of operations needed to write the letter Y on the grid given that in one operation you can change the value at any cell to 0, 1, or 2.

Example 1:

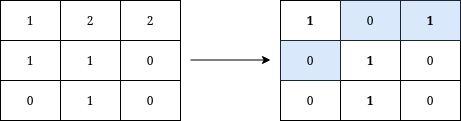
Input: grid = [[1,2,2],[1,1,0],[0,1,0]]
Output: 3
Explanation: We can write Y on the grid by applying the changes highlighted in blue in the image above. After the operations, all cells that belong to Y, denoted in bold, have the same value of 1 while those that do not belong to Y are equal to 0.
It can be shown that 3 is the minimum number of operations needed to write Y on the grid.

Example 2:

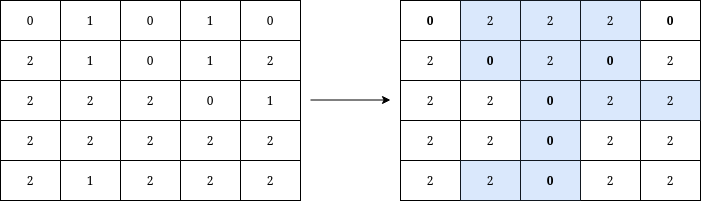
Input: grid = [[0,1,0,1,0],[2,1,0,1,2],[2,2,2,0,1],[2,2,2,2,2],[2,1,2,2,2]]
Output: 12
Explanation: We can write Y on the grid by applying the changes highlighted in blue in the image above. After the operations, all cells that belong to Y, denoted in bold, have the same value of 0 while those that do not belong to Y are equal to 2. 
It can be shown that 12 is the minimum number of operations needed to write Y on the grid.

Constraints:

3 <= n <= 49
n == grid.length == grid[i].length
0 <= grid[i][j] <= 2
n is odd.

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the dimensions of the grid? What is the data type of the grid values, and what values are considered 'on' vs 'off'?
Is the 'Y' we are trying to write a specific size or orientation, or are we allowed to choose the dimensions and position of the Y?
If it's impossible to write the 'Y' on the grid, what should the function return? (e.g., -1, null, or an exception?)
Can I assume the grid is rectangular, or could it be irregularly shaped?
What defines the 'Y' shape? Is it a specific pixel width for the stem and arms, and a defined angle between the arms?

Brute Force Solution

Approach

The problem asks us to find the fewest changes needed to draw the letter 'Y' on a grid. A brute force approach means trying every possible combination of changes to the grid cells until we find the one with the least amount of changes that successfully forms a 'Y'.

Here's how the algorithm would work step-by-step:

Imagine the grid is initially blank.
Start by trying to color in one cell at a time and check if that single cell forms a very small, incomplete version of the 'Y'.
Next, try all possible combinations of coloring in two cells, and then three, and so on.
For each combination of colored cells, check if it looks more and more like the letter 'Y'. To do this, we need to clearly define what the letter 'Y' should look like.
Keep going until we have tried coloring in every possible set of cells. Some combinations will look nothing like 'Y'. Some will almost resemble the letter 'Y'.
Also try removing colors from cells that are already colored if it makes the pattern look more like a 'Y'.
Count how many changes (coloring in or removing color from a cell) are needed for each combination that even remotely resembles a 'Y'.
After trying all possibilities, pick the combination that resulted in the fewest number of changes and also closely represents a 'Y'.

Code Implementation

def minimum_operations_y_brute_force(grid):
    rows = len(grid)
    cols = len(grid[0])
    min_operations = float('inf')

    for i in range(1 << (rows * cols)):
        temp_grid = [['.' for _ in range(cols)] for _ in range(rows)]
        operations = 0
        index = 0

        for row_index in range(rows):
            for col_index in range(cols):
                # Iterate through all possible combinations of cell changes
                if (i >> index) & 1:
                    if grid[row_index][col_index] == '.':
                        temp_grid[row_index][col_index] = 'X'
                        operations += 1
                    else:
                        temp_grid[row_index][col_index] = 'X'
                else:
                    if grid[row_index][col_index] == 'X':
                        operations += 1

                index += 1

        # Evaluate if the generated grid resembles a 'Y'
        if is_y_shape(temp_grid):
            min_operations = min(min_operations, operations)

    return min_operations

def is_y_shape(grid):
    rows = len(grid)
    cols = len(grid[0])
    
    # Define Y shape parameters. Adjust as needed
    stem_col = cols // 2
    fork_length = min(rows // 2, cols // 2)

    # Check for stem
    for row_index in range(rows // 2, rows):
        if grid[row_index][stem_col] != 'X':
            return False
    
    # Check for forking arms
    for row_index in range(rows // 2 - fork_length, rows // 2):
        left_col = stem_col - (rows // 2 - row_index)
        right_col = stem_col + (rows // 2 - row_index)

        if left_col >= 0 and grid[row_index][left_col] != 'X':
            return False
        if right_col < cols and grid[row_index][right_col] != 'X':
            return False

    return True

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(2^(n*n)) – The described brute force approach iterates through all possible combinations of colored and uncolored cells in the grid. If the grid has n rows and n columns, there are n*n cells. Each cell can be either colored or uncolored, leading to 2^(n*n) possible configurations of the grid. For each configuration, we check if it resembles a 'Y' and calculate the number of changes needed. Since we need to evaluate every single one of these configurations to find the minimum operations, the time complexity is O(2^(n*n)), which represents exponential time.

Space Complexity

O(1) – The described brute force approach primarily iterates through combinations of grid cells. While it considers coloring or removing colors from cells, it doesn't mention explicitly storing all possible combinations simultaneously. It appears to operate on one combination at a time, keeping track of the 'best' result so far. Therefore, beyond a few variables to track cell indices and the minimum operations, no auxiliary data structures that scale with the grid size (N, where N is implicitly the number of cells in the grid) are used. Hence, the auxiliary space complexity is O(1).

Optimal Solution

Approach

The best way to solve this is to think about building the 'Y' shape strategically, rather than trying every possibility. We will figure out the best way to draw each part of the 'Y' efficiently. This involves drawing the vertical line, then the two diagonal lines, minimizing the total number of operations.

Here's how the algorithm would work step-by-step:

First, consider where the center of the grid will be, as this is where the vertical and diagonal lines of the Y will meet.
Draw the vertical line of the 'Y' starting from the bottom row going up to the center.
Next, draw the diagonal line from the top-left corner of where it begins towards the center. Calculate the number of operations required for this line.
Now draw the other diagonal line, from the top-right corner of where it begins towards the center. Calculate the operations for this line.
Add up the operations used for the vertical line and both diagonal lines, avoiding double-counting any cell that's part of multiple lines. This is your minimum number of operations.

Code Implementation

def min_operations_to_write_y(grid):
    grid_size = len(grid)
    center_row = grid_size // 2
    center_column = grid_size // 2

    operations = 0

    # Draw the vertical line from bottom to center
    for row_index in range(center_row, grid_size):
        if grid[row_index][center_column] == 0:
            grid[row_index][center_column] = 1
            operations += 1

    # Draw the diagonal line from top-left to center
    for index in range(center_row):
        row_index = index
        column_index = index

        if grid[row_index][column_index] == 0:
            grid[row_index][column_index] = 1
            operations += 1

    # Draw the other diagonal line from top-right to center
    for index in range(center_row):
        row_index = index
        column_index = grid_size - 1 - index

        # Avoid recalculating for same cell
        if grid[row_index][column_index] == 0:
            grid[row_index][column_index] = 1
            operations += 1

    # Return the total number of operations
    return operations

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n) – The algorithm draws a vertical line, then two diagonal lines towards the center of the grid. Each of these lines' length is proportional to n, where n is the size of the grid. Specifically, the vertical line is of length n/2 and each diagonal line is proportional to n. Since we are only iterating through a number of cells proportional to n, and these are done sequentially (drawing one line after another), the time complexity is O(n).

Space Complexity

O(1) – The provided solution focuses on calculations based on the grid's center and does not involve storing the grid itself or creating additional data structures proportional to the grid size. The algorithm primarily uses a fixed number of variables to keep track of the operations and coordinates of the Y shape. Therefore, the auxiliary space used remains constant, independent of the input grid size, which implies a space complexity of O(1).

Edge Cases

Case	How to Handle
Zero-sized grid (n=0)	Return 0 as no operations are needed since there is no grid.
Small grid (n=1)	Check if the single cell is already 'Y', return 0 if so, 1 otherwise.
Grid already contains a perfect 'Y'	Return 0, as no operations are required.
All cells are the same and form the 'Y' shape	Handle the case where all cells are initialized to the color of the desired 'Y', returning 0.
Large grid (n is very large, potential for integer overflow)	Ensure the operation count uses a data type that can accommodate potentially large values, like long.
n is an even number.	The provided formula or logic must correctly handle even values of 'n' during coordinate calculations of the 'Y' shape's position, typically rounding appropriately.
Input grid is not square (rows != cols)	Return -1 or throw an exception, indicating that the problem is not valid or adapt to use min(rows, cols).
Memory Constraints on Large Grids	If modifying the grid in place is not feasible, an algorithm minimizing memory footprint by only considering key cells is required.