Number of Flowers in Full Bloom

Hard

Capital One

0 views

Topics:

ArraysBinary Search

You are given a 0-indexed 2D integer array flowers, where flowers[i] = [start_i, end_i] means the i^th flower will be in full bloom from start_i to end_i (inclusive). You are also given a 0-indexed integer array people of size n, where people[i] is the time that the i^th person will arrive to see the flowers.

Return an integer array answer of size n, where answer[i] is the number of flowers that are in full bloom when the i^th person arrives.

Example 1:

Input: flowers = [[1,6],[3,7],[9,12],[4,13]], people = [2,3,7,11]
Output: [1,2,2,2]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

Example 2:

Input: flowers = [[1,10],[3,3]], people = [3,3,2]
Output: [2,2,1]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

Constraints:

1 <= flowers.length <= 5 * 10⁴
flowers[i].length == 2
1 <= start_i <= end_i <= 10⁹
1 <= people.length <= 5 * 10⁴
1 <= people[i] <= 10⁹

Number of Flowers in Full Bloom

Hard

Capital One

0 views

Topics:

ArraysBinary Search

You are given a 0-indexed 2D integer array flowers, where flowers[i] = [start_i, end_i] means the i^th flower will be in full bloom from start_i to end_i (inclusive). You are also given a 0-indexed integer array people of size n, where people[i] is the time that the i^th person will arrive to see the flowers.

Return an integer array answer of size n, where answer[i] is the number of flowers that are in full bloom when the i^th person arrives.

Example 1:

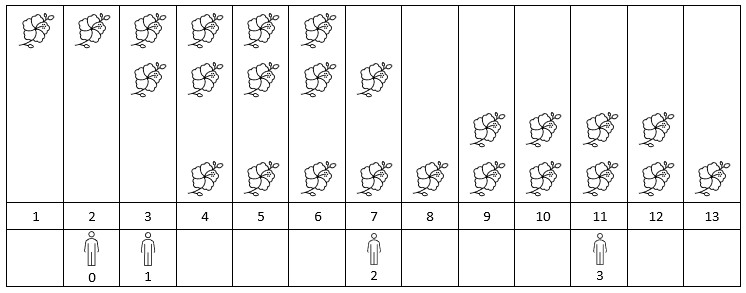
Input: flowers = [[1,6],[3,7],[9,12],[4,13]], people = [2,3,7,11]
Output: [1,2,2,2]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

Example 2:

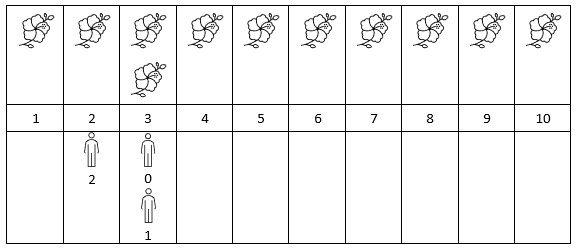
Input: flowers = [[1,10],[3,3]], people = [3,3,2]
Output: [2,2,1]
Explanation: The figure above shows the times when the flowers are in full bloom and when the people arrive.
For each person, we return the number of flowers in full bloom during their arrival.

Constraints:

1 <= flowers.length <= 5 * 10⁴
flowers[i].length == 2
1 <= start_i <= end_i <= 10⁹
1 <= people.length <= 5 * 10⁴
1 <= people[i] <= 10⁹

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What are the maximum possible values for `start_i`, `end_i`, and elements in the `people` array? Also, what are the maximum sizes of the `flowers` and `people` arrays?
Can the start day and end day of a flower be the same (i.e., `start_i == end_i`)? If so, is the flower considered to be in bloom only on that single day?
Is it possible for the start day of a flower to be later than the end day (i.e., `start_i > end_i`)? If so, how should I handle such cases?
If no flowers are in bloom for a particular person, should the corresponding element in the `answer` array be 0?
Are the `flowers` ranges guaranteed to be non-overlapping, or can they overlap?

Brute Force Solution

Approach

We want to find out how many flowers are in full bloom on certain days. The most basic approach is to check each day individually against every blooming period to see if it falls within that period.

Here's how the algorithm would work step-by-step:

For each day you want to check, take the first blooming period.
See if that day falls within the start and end date of that blooming period.
If it does, count one flower as blooming on that day.
Repeat this check for every blooming period available.
Once you've checked all blooming periods for that day, you know the total number of flowers in bloom on that specific day.
Repeat this entire process for every single day you need to check.

Code Implementation

def number_of_flowers_in_full_bloom_brute_force(flowers, people):
    number_of_flowers_per_person = []

    for person in people:
        flowers_blooming_for_current_person = 0

        # Iterate through each flower blooming period.
        for flower_start, flower_end in flowers:

            #Check if the person's arrival day is within bloom
            if flower_start <= person <= flower_end:
                flowers_blooming_for_current_person += 1

        number_of_flowers_per_person.append(flowers_blooming_for_current_person)

    return number_of_flowers_per_person

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n*m) – The algorithm iterates through each day in the input 'days' array, which we can define as having length 'n'. For each of these 'n' days, it then iterates through the 'flowers' array which has length 'm' to determine how many flowers are blooming on that specific day. Thus, for each of the 'n' days, we are doing 'm' operations, resulting in a time complexity of O(n*m).

Space Complexity

O(1) – The provided algorithm iterates through the bloom periods and days, but it does not create any auxiliary data structures whose size depends on the input. It uses a constant amount of space to store the count of blooming flowers for each day. Therefore, the auxiliary space complexity is O(1), indicating constant space usage regardless of the number of bloom periods or days to check.

Optimal Solution

Approach

To efficiently count blooming flowers for each person, we'll organize the flower blooming and closing times, then use a quick search to find how many flowers are blooming when each person arrives. This approach avoids checking every single flower for each person, making it much faster.

Here's how the algorithm would work step-by-step:

First, separate the blooming start times and the closing times of the flowers into two separate, sorted lists.
For each person's arrival time, find out how many flowers have started blooming by that time using a fast search method.
Then, also for each person's arrival time, find out how many flowers have already closed by that time, again using a fast search method.
Finally, for each person, subtract the number of closed flowers from the number of bloomed flowers to find the number of flowers blooming when they arrived.

Code Implementation

def number_of_flowers_in_full_bloom(flowers, people):
    start_times = sorted([flower[0] for flower in flowers])
    end_times = sorted([flower[1] for flower in flowers])

    result = []

    for person_arrival_time in people:
        # Find the number of flowers that have started blooming by this time.
        bloomed_count = find_highest_index_less_than_or_equal_to(
            start_times, person_arrival_time
        ) + 1

        # Find the number of flowers that have already closed by this time.
        closed_count = find_highest_index_less_than_or_equal_to(
            end_times, person_arrival_time
        ) + 1

        result.append(bloomed_count - closed_count)

    return result

def find_highest_index_less_than_or_equal_to(times, target_time):
    left_index = 0
    right_index = len(times) - 1
    highest_index = -1

    while left_index <= right_index:
        middle_index = (left_index + right_index) // 2

        if times[middle_index] <= target_time:
            # If the current middle time is less than target, it could be the answer,
            # but there might be a higher index that also satisfies condition.
            highest_index = middle_index
            left_index = middle_index + 1
        else:
            right_index = middle_index - 1

    return highest_index

Try it yourself on LeetCode

Big(O) Analysis

Time Complexity

O(n log n + m log n) – Sorting the bloom and end times takes O(n log n) time, where n is the number of flowers. For each person (m in total), we perform two binary searches on the sorted bloom and end times arrays, each taking O(log n) time. Therefore, the searches for all people take O(m log n) time. The overall time complexity is dominated by the sorting and the searches, resulting in O(n log n + m log n).

Space Complexity

O(N) – The algorithm creates two new lists to store the blooming start times and closing times of the flowers. In the worst case, these lists will contain all the blooming and closing times, resulting in a space usage proportional to the number of flowers, where N is the number of flowers (size of the input flowers array). Therefore, the auxiliary space complexity is O(N).

Edge Cases

Case	How to Handle
flowers is null or empty	Return an array of zeros with the same length as the people array, as no flowers are blooming.
people is null or empty	Return an empty array, as there are no people to check.
flowers contains very large start and end values (close to integer limit)	Ensure that calculations involving start and end values do not cause integer overflow by using appropriate data types (e.g., long).
All flowers bloom at the same time (same start and end)	The binary search algorithms or other approaches used to count blooming flowers should handle this case correctly by counting all these flowers when people arrive during this period.
Flowers blooming periods have large overlaps	The solution should correctly count the number of flowers blooming even with significant overlap using appropriate counting techniques.
people array has duplicate arrival times	The number of blooming flowers should be calculated correctly for each distinct arrival time, and duplicates should have identical counts in the output array.
start_i is greater than end_i for some flower	Handle this case as an invalid input, either by returning an error or treating the flower as not blooming at all (e.g., skip over this flower during processing).
The size of the input arrays are extremely large, potentially exceeding memory limits.	Ensure that the solution uses memory efficiently by avoiding unnecessary copies of large data structures and consider using in-place operations where possible or external sorting if the input cannot fit in memory.