Find the Largest Area of Square Inside Two Rectangles
MediumThere exist n rectangles in a 2D plane with edges parallel to the x and y axis. You are given two 2D integer arrays bottomLeft and topRight where bottomLeft[i] = [a_i, b_i] and topRight[i] = [c_i, d_i] represent the bottom-left and top-right coordinates of the ith rectangle, respectively.
You need to find the maximum area of a square that can fit inside the intersecting region of at least two rectangles. Return 0 if such a square does not exist.
Example 1:
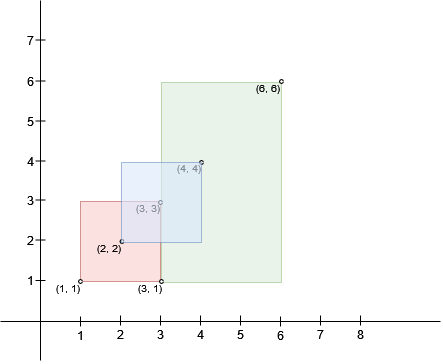
Input: bottomLeft = [[1,1],[2,2],[3,1]], topRight = [[3,3],[4,4],[6,6]]
Output: 1
Explanation:
A square with side length 1 can fit inside either the intersecting region of rectangles 0 and 1 or the intersecting region of rectangles 1 and 2. Hence the maximum area is 1. It can be shown that a square with a greater side length can not fit inside any intersecting region of two rectangles.
Example 2:
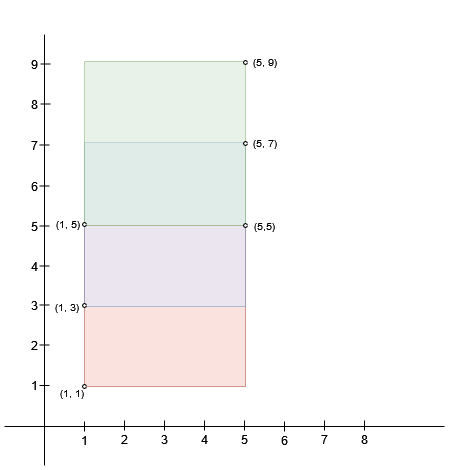
Input: bottomLeft = [[1,1],[1,3],[1,5]], topRight = [[5,5],[5,7],[5,9]]
Output: 4
Explanation:
A square with side length 2 can fit inside either the intersecting region of rectangles 0 and 1 or the intersecting region of rectangles 1 and 2. Hence the maximum area is 2 * 2 = 4. It can be shown that a square with a greater side length can not fit inside any intersecting region of two rectangles.
Example 3:
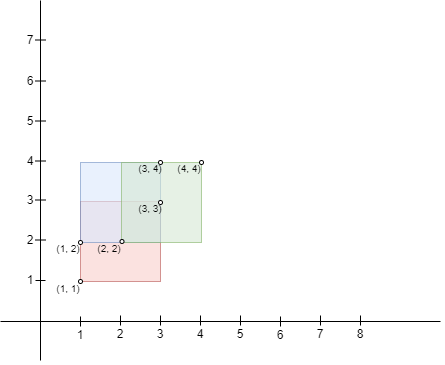
Input: bottomLeft = [[1,1],[2,2],[1,2]], topRight = [[3,3],[4,4],[3,4]]
Output: 1
Explanation:
A square with side length 1 can fit inside the intersecting region of any two rectangles. Also, no larger square can, so the maximum area is 1. Note that the region can be formed by the intersection of more than 2 rectangles.
Example 4:

Input: bottomLeft = [[1,1],[3,3],[3,1]], topRight = [[2,2],[4,4],[4,2]]
Output: 0
Explanation:
No pair of rectangles intersect, hence, the answer is 0.
Constraints:
n == bottomLeft.length == topRight.length2 <= n <= 103bottomLeft[i].length == topRight[i].length == 21 <= bottomLeft[i][0], bottomLeft[i][1] <= 1071 <= topRight[i][0], topRight[i][1] <= 107bottomLeft[i][0] < topRight[i][0]bottomLeft[i][1] < topRight[i][1]
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the format of the input? Specifically, how are the two rectangles represented (e.g., as a tuple of (x1, y1, x2, y2) coordinates where (x1, y1) is the top-left corner and (x2, y2) is the bottom-right)?
- Can the rectangles overlap, be disjoint, or be fully contained within each other?
- Can the sides of the rectangles be of length 0 (i.e., can x1 == x2 or y1 == y2)?
- If no square can be found within both rectangles, what should I return (e.g., 0, -1, null)?
- Are the coordinates integers or floating-point numbers? If integers, what's the range of values for the coordinates?
Brute Force Solution
Approach
To find the largest square inside two rectangles, the brute force method is like trying out every possible square size and location within both rectangles. We systematically check if each possible square fits completely inside both rectangles and remember the largest one we find.
Here's how the algorithm would work step-by-step:
- First, consider every possible size for a square, starting from a very small size and gradually increasing it.
- For each square size, try placing it at every possible position within the first rectangle. Imagine sliding the square around inside the first rectangle.
- If the square fits entirely inside the first rectangle, then check if that same square can also fit entirely inside the second rectangle. Again, imagine sliding the square around inside the second rectangle to find a position where it fits.
- If the square fits in both rectangles, remember its size. We want to keep track of the largest square size we've found so far that fits in both.
- Repeat the process for all possible square sizes and positions. Keep updating the size of the largest square we've found whenever we find a larger one that fits.
- After checking all possible square sizes and positions, the size we've remembered is the largest possible square that fits inside both rectangles.
Code Implementation
def find_largest_square_brute_force(rectangle1, rectangle2):
width_rectangle1 = rectangle1[0]
height_rectangle1 = rectangle1[1]
width_rectangle2 = rectangle2[0]
height_rectangle2 = rectangle2[1]
max_square_side = 0
# Iterate through possible square sizes.
for square_side in range(1, min(width_rectangle1, height_rectangle1, width_rectangle2, height_rectangle2) + 1):
# Check if square fits in the first rectangle.
for top_left_x_rectangle1 in range(width_rectangle1 - square_side + 1):
for top_left_y_rectangle1 in range(height_rectangle1 - square_side + 1):
# If it fits in the first rectangle, check the second
for top_left_x_rectangle2 in range(width_rectangle2 - square_side + 1):
for top_left_y_rectangle2 in range(height_rectangle2 - square_side + 1):
# Found a square that fits in both.
max_square_side = square_side
return max_square_sideBig(O) Analysis
Optimal Solution
Approach
The goal is to find the largest square that can fit completely inside the overlapping region of two rectangles. The most efficient strategy focuses on identifying the boundaries that limit the size of this square, rather than testing many square sizes.
Here's how the algorithm would work step-by-step:
- First, figure out the area where the two rectangles overlap. Think of it as finding the common ground between the rectangles.
- Determine the width and height of this overlapping area.
- The largest square that fits inside the overlap cannot be wider or taller than the overlap itself. The side length of the largest square is the smaller of the overlap's width and height.
- The area of this square is the side length multiplied by itself. This area is the largest possible square you can fit inside both rectangles.
Code Implementation
def find_largest_square_area(rectangle1, rectangle2):
x1_rectangle1, y1_rectangle1, x2_rectangle1, y2_rectangle1 = rectangle1
x1_rectangle2, y1_rectangle2, x2_rectangle2, y2_rectangle2 = rectangle2
# Find the coordinates of the overlapping rectangle
x_overlap_start = max(x1_rectangle1, x1_rectangle2)
y_overlap_start = max(y1_rectangle1, y1_rectangle2)
x_overlap_end = min(x2_rectangle1, x2_rectangle2)
y_overlap_end = min(y2_rectangle1, y2_rectangle2)
# If no overlap, return 0
if x_overlap_start >= x_overlap_end or y_overlap_start >= y_overlap_end:
return 0
overlap_width = x_overlap_end - x_overlap_start
overlap_height = y_overlap_end - y_overlap_start
# The largest square is limited by the smaller dimension.
side_length_of_square = min(overlap_width, overlap_height)
# Calculate the area of the largest possible square.
square_area = side_length_of_square * side_length_of_square
return square_areaBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or undefined input rectangles | Throw an IllegalArgumentException or return 0, indicating invalid input. |
| Rectangles with zero width or height | Treat these rectangles as invalid and return 0 since they enclose no area. |
| Rectangles with negative width or height | Treat negative dimensions as invalid and throw an exception or return 0. |
| Rectangles do not intersect | Return 0 since no square can be formed within the non-existent intersection. |
| One rectangle is fully contained within the other | The largest possible square side will be the minimum of the width and height of the inner rectangle. |
| Intersection forms a very narrow or tall rectangle | The maximum square size will be limited by the shorter dimension of the intersection rectangle. |
| Integer overflow potential when calculating intersection or square area | Use long data types or appropriate overflow handling techniques during calculations. |
| Floating-point precision issues with rectangle coordinates | Use appropriate tolerance when comparing coordinates or consider using integer representation for coordinates. |