Find Common Elements Between Two Arrays
EasyYou are given two integer arrays nums1 and nums2 of sizes n and m, respectively. Calculate the following values:
answer1: the number of indicesisuch thatnums1[i]exists innums2.answer2: the number of indicesisuch thatnums2[i]exists innums1.
Return [answer1,answer2].
Example 1:
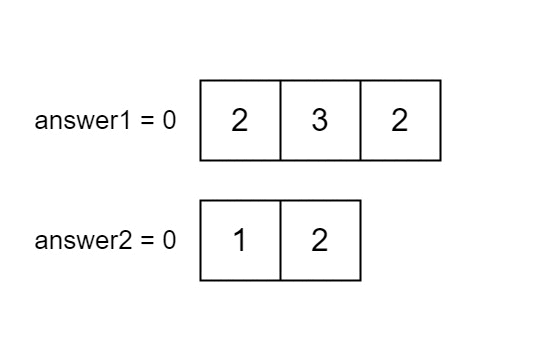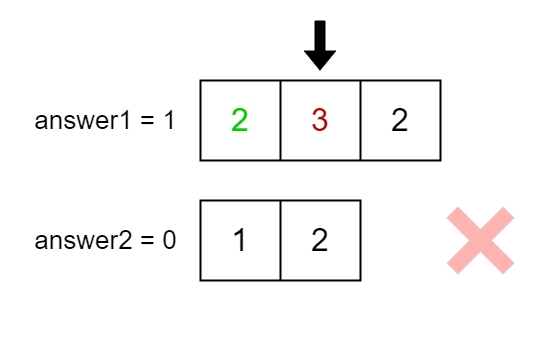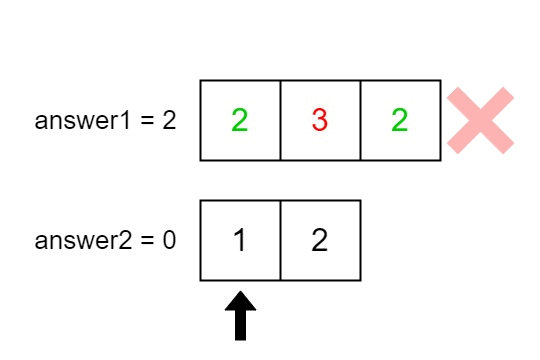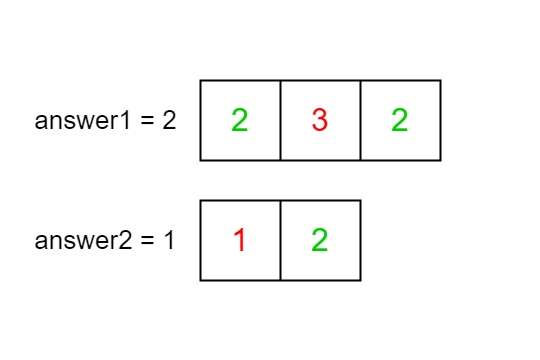
Input: nums1 = [2,3,2], nums2 = [1,2]
Output: [2,1]
Explanation:
Example 2:
Input: nums1 = [4,3,2,3,1], nums2 = [2,2,5,2,3,6]
Output: [3,4]
Explanation:
The elements at indices 1, 2, and 3 in nums1 exist in nums2 as well. So answer1 is 3.
The elements at indices 0, 1, 3, and 4 in nums2 exist in nums1. So answer2 is 4.
Example 3:
Input: nums1 = [3,4,2,3], nums2 = [1,5]
Output: [0,0]
Explanation:
No numbers are common between nums1 and nums2, so answer is [0,0].
Constraints:
n == nums1.lengthm == nums2.length1 <= n, m <= 1001 <= nums1[i], nums2[i] <= 100
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the expected behavior if either or both of the input arrays are null or empty?
- Can the input arrays contain duplicate numbers, and if so, how should duplicates be handled in the output? Specifically, should I return the common element as many times as it appears in both arrays, or only once?
- What is the range of possible integer values within the input arrays?
- Is the order of the common elements in the output array important?
- Do you have any concerns about the memory usage given the potential size of the input arrays?
Brute Force Solution
Approach
The brute force method for finding common items in two lists is like comparing each item from one list to every item in the other list. We systematically check all possible pairs to see if they match. It's a straightforward, though perhaps slow, way to find what's shared between the lists.
Here's how the algorithm would work step-by-step:
- Take the first item from the first list.
- Compare this item to every single item in the second list, one by one.
- If you find a match, remember that item as a common element.
- Now, move to the second item in the first list.
- Again, compare this second item to every single item in the second list.
- Repeat this process for every item in the first list, comparing it to every item in the second list each time.
- At the end, you'll have a collection of all the items that were found in both lists.
Code Implementation
def find_common_elements_brute_force(first_array, second_array):
common_elements = []
for first_array_element in first_array:
# Iterate through the second array
for second_array_element in second_array:
# Compare the elements to see if they match
if first_array_element == second_array_element:
# Only add the element if it's not already in the result
if first_array_element not in common_elements:
common_elements.append(first_array_element)
return common_elementsBig(O) Analysis
Optimal Solution
Approach
The most efficient way to find common elements is to first organize one of the collections to allow for quick lookups. Then, we check each element from the other collection against this organized structure to identify the shared elements.
Here's how the algorithm would work step-by-step:
- First, take one of the collections and convert it into a structure that makes it easy to check if an element exists.
- Go through the second collection, one item at a time.
- For each item in the second collection, check if it's present in the organized structure we created from the first collection.
- If the item exists in both, record it as a common element.
- Continue until all items in the second collection have been checked.
- The recorded common elements are the result.
Code Implementation
def find_common_elements(first_array, second_array):
# Use a set for fast lookups
first_array_set = set(first_array)
common_elements = []
# Iterate through the second array
for element_in_second_array in second_array:
# Check for element's existence
if element_in_second_array in first_array_set:
# Record the common element
common_elements.append(element_in_second_array)
return common_elementsBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Both input arrays are null | Return an empty list or throw an IllegalArgumentException, depending on requirements, to avoid NullPointerException. |
| One input array is null while the other is not | Return an empty list, assuming no common elements exist with a null array. |
| Both input arrays are empty | Return an empty list as there are no elements to compare. |
| One input array is empty while the other is not | Return an empty list, since an empty array cannot have any common elements with another array. |
| Arrays contain duplicate elements with varying frequencies | Using a HashMap to track element counts in both arrays ensures that only the minimum number of occurrences are included in the result. |
| Arrays contain very large integers approaching integer limits | Ensure the data structures used (HashMap, etc.) can accommodate large integer values without overflow. |
| Arrays contain negative integers | The solution should handle negative numbers correctly, as integer comparisons and hashmap lookups work for negative values. |
| Arrays are extremely large, potentially exceeding available memory if the intersection is large | Consider using external memory algorithms or techniques to process arrays in chunks if memory becomes a constraint. |