Find the Safest Path in a Grid

#235 Most AskedMedium

Find the Safest Path in a Grid #235 Most Asked

Medium

Amazon

9 views

Topics:

ArraysBinary SearchGraphs

You are given a 0-indexed 2D matrix grid of size n x n, where (r, c) represents:

A cell containing a thief if grid[r][c] = 1
An empty cell if grid[r][c] = 0

You are initially positioned at cell (0, 0). In one move, you can move to any adjacent cell in the grid, including cells containing thieves.

The safeness factor of a path on the grid is defined as the minimum manhattan distance from any cell in the path to any thief in the grid.

Return the maximum safeness factor of all paths leading to cell (n - 1, n - 1).

An adjacent cell of cell (r, c), is one of the cells (r, c + 1), (r, c - 1), (r + 1, c) and (r - 1, c) if it exists.

The Manhattan distance between two cells (a, b) and (x, y) is equal to |a - x| + |b - y|, where |val| denotes the absolute value of val.

Example 1:

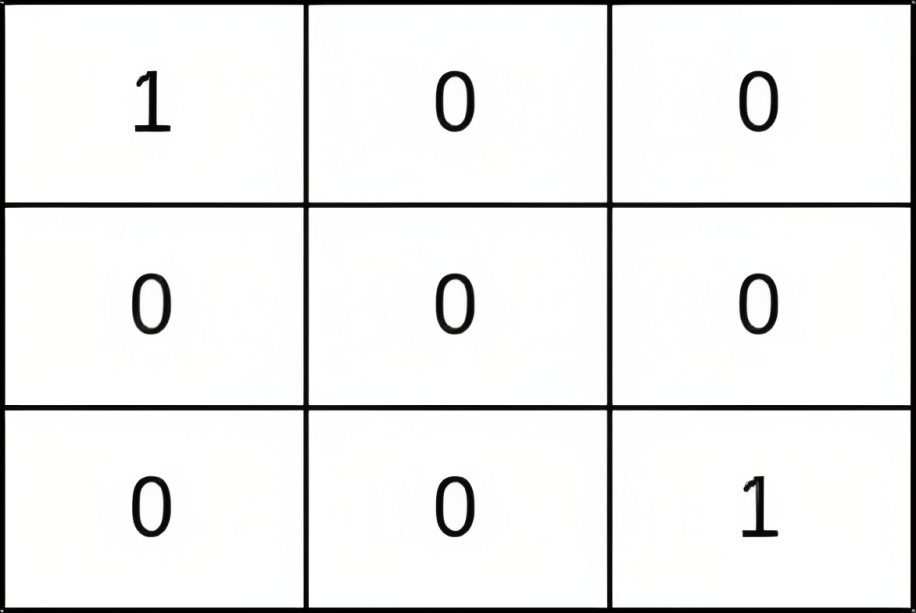
Input: grid = [[1,0,0],[0,0,0],[0,0,1]]
Output: 0
Explanation: All paths from (0, 0) to (n - 1, n - 1) go through the thieves in cells (0, 0) and (n - 1, n - 1).

Example 2:

Input: grid = [[0,0,1],[0,0,0],[0,0,0]]
Output: 2
Explanation: The path depicted in the picture above has a safeness factor of 2 since:
- The closest cell of the path to the thief at cell (0, 2) is cell (0, 0). The distance between them is | 0 - 0 | + | 0 - 2 | = 2.
It can be shown that there are no other paths with a higher safeness factor.

Example 3:

Input: grid = [[0,0,0,1],[0,0,0,0],[0,0,0,0],[1,0,0,0]]
Output: 2
Explanation: The path depicted in the picture above has a safeness factor of 2 since:
- The closest cell of the path to the thief at cell (0, 3) is cell (1, 2). The distance between them is | 0 - 1 | + | 3 - 2 | = 2.
- The closest cell of the path to the thief at cell (3, 0) is cell (3, 2). The distance between them is | 3 - 3 | + | 0 - 2 | = 2.
It can be shown that there are no other paths with a higher safeness factor.

Constraints:

1 <= grid.length == n <= 400
grid[i].length == n
grid[i][j] is either 0 or 1.
There is at least one thief in the grid.

Try coding it in LeetCode

Solution

Clarifying Questions

When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:

What range of values can 'risk' have, and can it be negative or zero?
What should I return if there is no path from the top-left to the bottom-right?
Is the grid guaranteed to be rectangular, or can the rows have different lengths?
Can the starting cell (top-left) or ending cell (bottom-right) have a risk value that prevents a path from existing, like a very high risk value?
By 'safest path', do you mean the path with the minimum *maximum* risk value among all the cells in that path, or something else (e.g., minimizing the sum of risks)?
Is there a limit to the grid dimensions?

Brute Force Solution

Approach

The brute-force approach to finding the safest path is like exploring every single route in the grid. We try every possible path from the start to the end, one at a time. Then we compare all the paths and pick the safest one based on the danger levels we encounter along the way.

Here's how the algorithm would work step-by-step:

Start at the beginning of the grid.
Consider all possible directions you can move from your current spot (like up, down, left, or right).
For each direction, imagine taking that step and marking the new location as part of a potential path.
Keep doing this, adding more and more steps, until you reach the end of the grid.
Every time you reach the end, remember the danger levels you encountered along that specific path.
After trying every single possible path from the beginning to the end, compare the overall danger level of each path.
The path with the lowest total danger is the safest path.

Code Implementation

def find_safest_path_brute_force(grid):
    rows = len(grid)
    cols = len(grid[0])
    all_paths_danger = []

    def explore_path(row, col, current_path_danger):
        # If we reached the end of the grid, record the total danger
        if row == rows - 1 and col == cols - 1:
            all_paths_danger.append(current_path_danger + grid[row][col])
            return

        # Check boundaries and explore possible paths
        if row < 0 or row >= rows or col < 0 or col >= cols:
            return

        # Prevents re-visiting and infinite loops.
        new_path_danger = current_path_danger + grid[row][col]

        # Explore downwards
        explore_path(row + 1, col, new_path_danger)

        # Explore rightwards
        explore_path(row, col + 1, new_path_danger)

    explore_path(0, 0, 0)

    # Find the path with the minimum danger level
    if not all_paths_danger:
        return -1

    return min(all_paths_danger)

Big(O) Analysis

Time Complexity

O(4^(m+n)) – In the brute-force approach, we explore all possible paths from the top-left to the bottom-right corner of an m x n grid. At each cell, we can move either right or down, leading to a branching factor of 2. Since the shortest path requires m+n steps, a simplified estimate of total paths is 2^(m+n). However, in a grid, we can also revisit previously visited cells. Since we can move up, down, left, or right, the branching factor at each cell is effectively 4. Thus, the number of possible paths grows exponentially with the size of the grid, resulting in a time complexity of roughly O(4^(m+n)), where m and n are the dimensions of the grid.

Space Complexity

O(4^N) – The brute-force approach explores every possible path from start to end using recursion. In the worst-case scenario, at each cell, we might have up to 4 possible directions to explore (up, down, left, right) assuming we are not revisiting cells. If the grid is of size N (where N is the number of cells), then the maximum depth of the recursion can be N. Thus, the number of paths explored grows exponentially as 4^N in the worst case. Each recursive call requires stack space, therefore the space complexity is O(4^N) to store all function calls in the call stack.

Optimal Solution

Approach

The goal is to find the path through a grid that avoids the most dangerous cells. We want to find the route with the highest possible minimum safety value. We can efficiently do this by thinking about safety as a value we want to maximize at each cell.

Here's how the algorithm would work step-by-step:

Imagine each cell in the grid has a 'safety score' indicating how dangerous it is.
We want to figure out, for each cell, what the highest possible 'minimum safety' is to reach that cell from the starting point.
Start by giving the starting cell its own safety score.
Now, look at the cells next to the starting cell. The 'safest path' to them is the one that either comes directly from the start, or some other existing path.
When moving to a neighboring cell, the 'minimum safety' of the path becomes the smaller of the current cell's safety value, and the best 'minimum safety' value of the cell we are coming from. We only move in down or right directions.
Keep repeating this process for all cells, moving from top-left to bottom-right. We always choose the safest path to get to the current cell.
By the time we reach the end cell, we will have found the path with the highest possible 'minimum safety' score, which is what we wanted to find.

Code Implementation

def find_safest_path(risk_grid):
    grid_height = len(risk_grid)
    grid_width = len(risk_grid[0])
    safest_path_values = [([0] * grid_width) for _ in range(grid_height)]

    safest_path_values[0][0] = risk_grid[0][0]

    for row_index in range(grid_height): 
        for column_index in range(grid_width):

            if row_index == 0 and column_index == 0:
                continue

            max_safety_value = -1

            # Check path from top
            if row_index > 0:
                max_safety_value = max(max_safety_value, min(safest_path_values[row_index-1][column_index], risk_grid[row_index][column_index]))

            # Check path from left
            if column_index > 0:
                max_safety_value = max(max_safety_value, min(safest_path_values[row_index][column_index-1], risk_grid[row_index][column_index]))

            safest_path_values[row_index][column_index] = max_safety_value

    # The last cell holds the overall safest path value.
    return safest_path_values[grid_height-1][grid_width-1]

Big(O) Analysis

Time Complexity

O(n*m) – The algorithm iterates through each cell in the grid once to calculate the maximum minimum safety score to reach that cell. Given a grid of size n rows and m columns, the algorithm visits each cell once. Therefore, the time complexity is proportional to the number of cells in the grid, resulting in O(n*m). If n and m were equal, then this would simplify to O(n^2).

Space Complexity

O(N) – The algorithm implicitly uses a grid (or a similar data structure) of the same dimensions as the input grid to store the highest possible minimum safety values for each cell. Where N represents the total number of cells in the input grid. This auxiliary grid is used to keep track of intermediate results as we traverse the grid. Therefore, the space complexity is directly proportional to the number of cells in the grid, resulting in O(N) space.

Edge Cases

Case	How to Handle
Null or empty grid	Return an empty path or an error code, indicating no path exists.
Grid with only one cell	If the single cell is safe, return a path containing only that cell; otherwise, return an empty path.
Grid with no safe cells (all cells are dangerous)	Return an empty path or an error code signifying no safe path is available.
Start or end cell is dangerous	Return an empty path, as a path starting or ending at a dangerous cell is invalid.
Grid contains negative risk values	Handle negative risk values appropriately, ensuring they don't negatively impact the safety calculation.
Integer overflow when calculating path risk	Use a data type with sufficient range (e.g., long) or modulo arithmetic to prevent integer overflow.
No path exists between start and end cells	Return an empty path or an error code if no path is found after exploring all possibilities.
Large grid dimensions leading to memory issues	Consider using iterative approaches like BFS or A* search to manage memory usage, avoiding excessive recursion.

Null or empty grid

How to Handle:

Return an empty path or an error code, indicating no path exists.

Grid with only one cell

How to Handle:

If the single cell is safe, return a path containing only that cell; otherwise, return an empty path.

Grid with no safe cells (all cells are dangerous)

How to Handle:

Return an empty path or an error code signifying no safe path is available.

Start or end cell is dangerous

How to Handle:

Return an empty path, as a path starting or ending at a dangerous cell is invalid.

Grid contains negative risk values

How to Handle:

Handle negative risk values appropriately, ensuring they don't negatively impact the safety calculation.

Integer overflow when calculating path risk

How to Handle:

Use a data type with sufficient range (e.g., long) or modulo arithmetic to prevent integer overflow.

No path exists between start and end cells

How to Handle:

Return an empty path or an error code if no path is found after exploring all possibilities.

Large grid dimensions leading to memory issues

How to Handle:

Consider using iterative approaches like BFS or A* search to manage memory usage, avoiding excessive recursion.