Maximum Difference Between Node and Ancestor
MediumGiven the root of a binary tree, find the maximum value v for which there exist different nodes a and b where v = |a.val - b.val| and a is an ancestor of b.
A node a is an ancestor of b if either: any child of a is equal to b or any child of a is an ancestor of b.
Example 1:
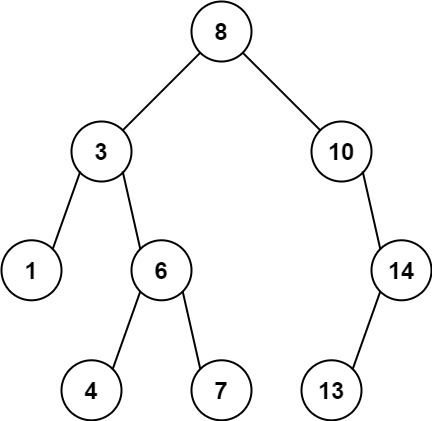
Input: root = [8,3,10,1,6,null,14,null,null,4,7,13] Output: 7 Explanation: We have various ancestor-node differences, some of which are given below : |8 - 3| = 5 |3 - 7| = 4 |8 - 1| = 7 |10 - 13| = 3 Among all possible differences, the maximum value of 7 is obtained by |8 - 1| = 7.
Example 2:
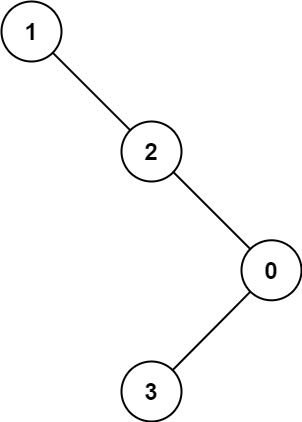
Input: root = [1,null,2,null,0,3] Output: 3
Constraints:
- The number of nodes in the tree is in the range
[2, 5000]. 0 <= Node.val <= 105
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for the nodes in the tree? Can the values be negative?
- Can the tree be empty, or contain only one node? What should I return in those cases?
- Is the input a valid binary tree, or do I need to handle cases where the tree structure is invalid?
- If there are multiple node-ancestor pairs with the same maximum difference, can I return any one of them, or is there a preference?
- Are node values guaranteed to be integers, or could they be floating-point numbers?
Brute Force Solution
Approach
To find the biggest difference between a tree node and one of its ancestors (a node above it), we can check every single possible pair. The brute force way means we leave no stone unturned.
Here's how the algorithm would work step-by-step:
- Start with the very first node in the tree.
- For that node, go through every node above it (its ancestors) one by one.
- Calculate the difference between the starting node and each of its ancestors.
- Keep track of the biggest difference we've seen so far.
- Move on to the next node in the tree and repeat the process, comparing it to all its ancestors.
- Continue doing this for every single node in the entire tree.
- In the end, the largest difference you tracked is the answer.
Code Implementation
def max_ancestor_diff_brute_force(root):
max_difference = 0
def get_all_nodes(root_node):
if not root_node:
return []
return [root_node] + get_all_nodes(root_node.left) + get_all_nodes(root_node.right)
all_nodes = get_all_nodes(root)
def get_ancestors(node, root_node):
ancestors = []
def traverse(current_node, path):
if not current_node:
return
if current_node == node:
ancestors.extend(path)
return
traverse(current_node.left, path + [current_node])
traverse(current_node.right, path + [current_node])
traverse(root_node, [])
return ancestors
for node in all_nodes:
ancestors = get_ancestors(node, root)
# Iterate through all ancestors of the current node.
for ancestor in ancestors:
difference = abs(node.val - ancestor.val)
# Keep track of the largest difference found.
max_difference = max(max_difference, difference)
return max_differenceBig(O) Analysis
Optimal Solution
Approach
The best way to solve this problem is to keep track of the largest and smallest values you've seen so far as you travel down the tree. At each stop, we'll compare the current node's value to those maximum and minimum ancestor values to see if we've found a new biggest difference.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree.
- As you go down to each node, remember the biggest and smallest numbers you've seen on the path from the top to that node.
- At each node, find the difference between the node's value and the biggest value you've seen so far, and the difference between the node's value and the smallest value you've seen so far.
- Keep track of the largest of all those differences you've found. This is your answer.
- When you explore the next branch, carry along the current maximum and minimum values you've seen down the path so far. That means the new node will have access to the largest and smallest values of its ancestors.
- By keeping track of the largest and smallest ancestors as we traverse the tree, we can calculate the maximum difference efficiently.
Code Implementation
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def maxAncestorDiff(root):
maximum_difference = 0
def dfs(node, current_max, current_min):
nonlocal maximum_difference
if not node:
return
# Update the max difference with current node.
maximum_difference = max(maximum_difference, abs(node.val - current_max), abs(node.val - current_min))
# Update the running maximum and minimum.
new_max = max(current_max, node.val)
new_min = min(current_min, node.val)
# Explore left and right subtrees,
# passing down the updated max and min.
dfs(node.left, new_max, new_min)
dfs(node.right, new_max, new_min)
# Start DFS with initial max and min as root's value.
dfs(root, root.val, root.val)
return maximum_differenceBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null root node | Return 0 immediately as there are no nodes to compare. |
| Single node tree | Return 0 because a single node has no ancestor other than itself. |
| Tree with all nodes having the same value | The maximum difference will be 0 as all nodes are identical. |
| Deeply skewed tree (all nodes on one branch) | The algorithm should still correctly traverse this tree, potentially having greater stack depth if recursion is used, but the algorithm's time complexity remains unaffected, provided it uses a valid traversal strategy. |
| Tree with large positive and negative values | Ensure the difference calculation doesn't result in integer overflow; use a larger data type if necessary (e.g., long). |
| Binary Search Tree with small values on the left and large on the right | This is a normal case that should be handled by the standard traversal. |
| Large tree nearing memory limits | If recursion is used, consider iterative DFS to avoid stack overflow errors; or explore algorithms requiring lower memory footprint. |
| Perfectly balanced tree | This is a normal case and will be processed without issues; no special handling is needed. |