Minimum Cuts to Divide a Circle
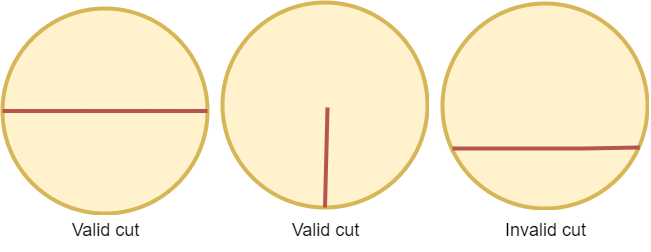
EasyA valid cut in a circle can be:
- A cut that is represented by a straight line that touches two points on the edge of the circle and passes through its center, or
- A cut that is represented by a straight line that touches one point on the edge of the circle and its center.
Some valid and invalid cuts are shown in the figures below.
Given the integer n, return the minimum number of cuts needed to divide a circle into n equal slices.
Example 1:
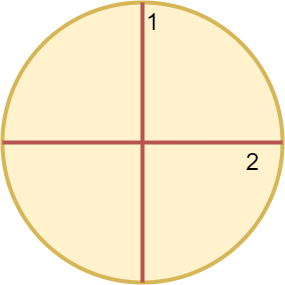
Input: n = 4 Output: 2 Explanation: The above figure shows how cutting the circle twice through the middle divides it into 4 equal slices.
Example 2:

Input: n = 3 Output: 3 Explanation: At least 3 cuts are needed to divide the circle into 3 equal slices. It can be shown that less than 3 cuts cannot result in 3 slices of equal size and shape. Also note that the first cut will not divide the circle into distinct parts.
Constraints:
1 <= n <= 100
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What data type will represent the number of cuts, and what is the maximum possible number of cuts that I should consider?
- Is the circle assumed to be a perfect mathematical circle (i.e., can I assume no floating-point errors in calculations involving angles and distances)?
- Can the number of cuts be zero or negative? If so, what should the function return in those cases?
- Are there any restrictions on where the cuts should be placed (e.g., must they be equally spaced, or can they be at any arbitrary point on the circle's circumference)?
- Is the input simply the number of cuts or are there additional constraints or parameters related to the cuts (e.g., locations or types of cuts required)?
Brute Force Solution
Approach
The brute force way to find the minimum cuts is to try every single possible way to divide the circle with lines. We then count how many cuts each way takes and choose the one with the fewest cuts. It's like trying every possibility, no matter how silly.
Here's how the algorithm would work step-by-step:
- Start with zero cuts and see if that divides the circle into the required number of pieces. If it does, we're done!
- If zero cuts doesn't work, try making one cut. See if there's any single cut that results in the required number of pieces.
- If one cut doesn't work, try making two cuts. Check every possible pair of cuts to see if they result in the required number of pieces.
- Continue this process, adding one more cut at a time, and checking *every* possible combination of cuts at that number. For each new cut, we check *all* possible positions for that cut relative to the existing cuts.
- Keep going until we find a set of cuts that divides the circle into exactly the number of pieces we need.
- The smallest number of cuts we found that works is our answer.
Code Implementation
def minimum_cuts_brute_force(number_of_pieces_needed):
for number_of_cuts in range(number_of_pieces_needed + 1):
number_of_pieces = (number_of_cuts * (number_of_cuts + 1)) // 2 + 1
# If we find a valid cut, return the number of cuts immediately
if number_of_pieces == number_of_pieces_needed:
return number_of_cuts
# If number of pieces exceeds needed, cannot work
if number_of_pieces > number_of_pieces_needed:
break
# If no solution is found, return -1.
return -1Big(O) Analysis
Optimal Solution
Approach
The problem asks for the fewest straight lines to cut a circle into a certain number of pieces. The key insight is that the more lines intersect inside the circle, the more pieces you create with each new line. The optimal strategy therefore is to maximize intersections.
Here's how the algorithm would work step-by-step:
- If you want only one piece, you don't need any cuts.
- If you want two pieces, you only need one cut that goes straight across the circle.
- For more than two pieces, start by drawing a cut straight across the circle. All further cuts should also go straight across the circle.
- Make sure each new cut crosses all the previous cuts inside the circle. This ensures each new line creates the maximum number of new pieces.
- The number of pieces increases by the number of intersections plus one with each new cut. So keep adding lines this way until you reach the number of pieces you want.
- The total number of cuts you made to reach the desired number of pieces is your answer.
Code Implementation
def min_cuts_to_divide_circle(number_of_pieces):
if number_of_pieces == 1:
return 0
if number_of_pieces == 2:
return 1
number_of_cuts = 1
total_pieces = 2
# We start with one cut and two pieces.
# Subsequent cuts intersect all previous cuts.
while total_pieces < number_of_pieces:
number_of_cuts += 1
# Each new cut adds intersections + 1 pieces
total_pieces += (number_of_cuts - 1) + 1
# Terminate early if target reached
if total_pieces >= number_of_pieces:
break
# Return the min number of cuts.
return number_of_cutsBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Zero cuts required | If the number of points is 1, return 0 since no cuts are needed. |
| One cut required | If the number of points is 2, return 1 since one cut is sufficient. |
| Integer overflow for large input | The problem's constraints should prevent integer overflow, but if inputs are very large, using long data types to store number of points ensures safe computation. |
| Negative number of cuts not possible | The number of points cannot be negative, so the code should either throw an exception or return a reasonable default value (e.g., 0) if the input is invalid. |
| Even number of points | For an even number of points, the number of cuts is equal to the number of points divided by 2. |
| Odd number of points | For an odd number of points, the number of cuts is equal to the number of points since each point must be connected to its direct opposite requiring a cut through each. |
| Maximum number of points allowed by integer type | Verify that the input does not exceed the maximum value allowed for the integer data type to prevent unexpected behavior, and use appropriate data type. |
| Edge case where n = 2147483647 (max int) | Ensure correct behavior by using int (or long as needed), and avoid calculations that may lead to overflow during the division operation |