Remove Duplicates from Sorted List II
MediumGiven the head of a sorted linked list, delete all nodes that have duplicate numbers, leaving only distinct numbers from the original list. Return the linked list sorted as well.
Example 1:
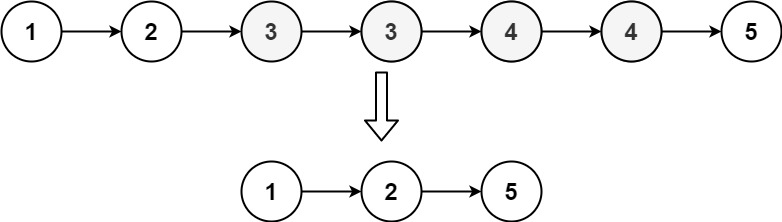
Input: head = [1,2,3,3,4,4,5] Output: [1,2,5]
Example 2:
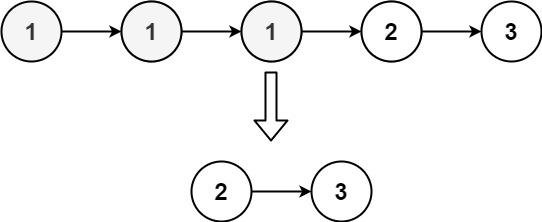
Input: head = [1,1,1,2,3] Output: [2,3]
Constraints:
- The number of nodes in the list is in the range
[0, 300]. -100 <= Node.val <= 100- The list is guaranteed to be sorted in ascending order.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values for the integers in the linked list?
- Can the input list be empty or null?
- If all nodes in the list have duplicate values, should I return an empty list (null head)?
- Is the list guaranteed to be sorted in ascending order, or could it be descending?
- Can I modify the original list in place, or do I need to create a new list?
Brute Force Solution
Approach
The brute force approach to removing duplicate nodes from a sorted list involves checking every node to see if it's part of a sequence of duplicate values. If it is, we skip over the entire sequence when building our new list. Otherwise, we keep the node and add it to our new list.
Here's how the algorithm would work step-by-step:
- Start at the beginning of the list.
- For each node, check if it has any identical neighbors by looking at the following nodes.
- If the current node is part of a sequence of duplicate values, find the very end of that sequence.
- Jump over the entire sequence of duplicate values to the node after the last duplicate.
- If the current node is not part of a sequence of duplicate values, keep that node.
- Add the kept nodes to form a new list.
- Continue this process until the end of the original list is reached.
- The resulting list will have all the duplicate sequences removed.
Code Implementation
def remove_duplicates_from_sorted_list_ii_brute_force(head):
dummy_node = ListNode(0)
tail_of_new_list = dummy_node
current_node = head
while current_node:
# Check for duplicate sequence
if current_node.next and current_node.val == current_node.next.val:
duplicate_value = current_node.val
# Advance to the end of the duplicate sequence
while current_node and current_node.val == duplicate_value:
current_node = current_node.next
else:
# Attach node because it's unique
tail_of_new_list.next = current_node
tail_of_new_list = tail_of_new_list.next
current_node = current_node.next
# Terminate the new list
tail_of_new_list.next = None
return dummy_node.next
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = nextBig(O) Analysis
Optimal Solution
Approach
The goal is to go through a sorted list and remove any numbers that appear more than once. The optimal approach involves carefully checking each number and linking around any sequence of repeated numbers, avoiding the need to repeatedly search the list.
Here's how the algorithm would work step-by-step:
- Start by creating a 'dummy' number before the beginning of the list. This makes handling the first number easier.
- Keep track of the number you're currently examining, as well as the number before that.
- Go through the list one number at a time.
- If the current number is the same as the next number, then you've found a sequence of duplicate numbers. Keep going through the list until the duplicate numbers stop.
- If, after finding a duplicate sequence, the current number is also equal to the number before it, then you know you've got to remove all duplicate sequences, so link the node before the sequence of duplicates to the first node after the sequence of duplicates.
- Move on to the next number and repeat steps 4 and 5 until you've reached the end of the list.
- Return the list starting from the number right after the 'dummy' number, since the dummy number does not actually exist in the list.
Code Implementation
class ListNode:
def __init__(self, val=0, next=None):
self.val = val
self.next = next
def remove_duplicates_from_sorted_list_ii(head):
dummy_node = ListNode(0)
dummy_node.next = head
previous_node = dummy_node
current_node = head
while current_node:
# Check for duplicates by comparing current with next
if current_node.next and current_node.val == current_node.next.val:
# Found duplicate sequence
# Move past all duplicates
while current_node.next and current_node.val == current_node.next.val:
current_node = current_node.next
# Need to skip duplicate sequence
previous_node.next = current_node.next
else:
# No duplicates, move along
previous_node = current_node
current_node = current_node.next
# Return list starting after dummy node
return dummy_node.nextBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Empty list (head is null) | Return null immediately as there are no nodes to process. |
| List with a single node | Return the head directly, as a single node cannot have duplicates. |
| List with only two nodes and they are duplicates | Return null as both nodes must be removed. |
| List with only two nodes and they are distinct | Return the original head as no duplicates exist. |
| List with all nodes having the same value | Return null as all nodes are duplicates and must be removed. |
| Duplicates at the beginning of the list | The dummy node handles removal of the initial duplicated node(s) correctly. |
| Duplicates at the end of the list | The algorithm correctly identifies and removes the trailing duplicates. |
| Large list with many duplicate sequences | The iterative approach ensures the solution can handle large lists efficiently without stack overflow issues. |