Maximum Depth of N-ary Tree
EasyGiven a n-ary tree, find its maximum depth.
The maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.
Nary-Tree input serialization is represented in their level order traversal, each group of children is separated by the null value (See examples).
Example 1:

Input: root = [1,null,3,2,4,null,5,6] Output: 3
Example 2:
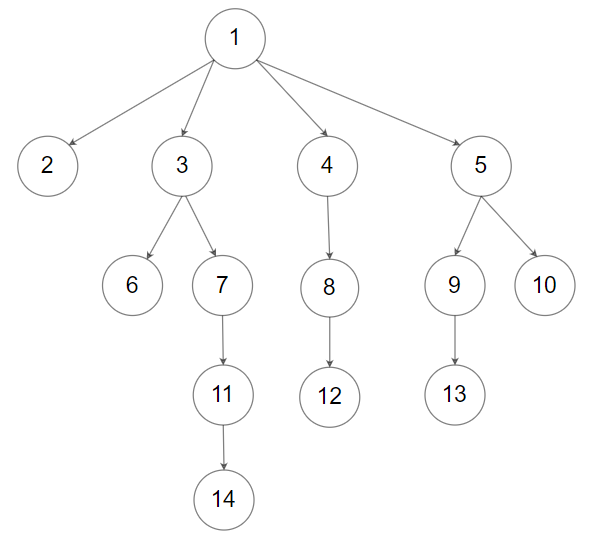
Input: root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] Output: 5
Constraints:
- The total number of nodes is in the range
[0, 104]. - The depth of the n-ary tree is less than or equal to
1000.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Can the N-ary tree be empty (i.e., root is null)? If so, what should I return?
- What is the maximum number of children a node can have in the N-ary tree? Is there a practical limit?
- Are the node values relevant to determining the depth, or do I only need to consider the tree structure?
- Can I assume that the tree is a valid N-ary tree structure, or do I need to handle cases where the tree is malformed (e.g., cycles)?
- What data type are the node values? (Although likely irrelevant for depth calculation, it's good to confirm)
Brute Force Solution
Approach
To find the maximum depth of a tree, the brute force method explores every possible path from the root to a leaf. We will visit each branch completely and count how many levels we go down in each case. The longest of these paths will be our answer.
Here's how the algorithm would work step-by-step:
- Begin at the very top of the tree, the root.
- Look at each of its immediate children one by one.
- For each child, go down one level and count that level.
- Then, look at each of that child's children and do the same, adding to the level count.
- Continue going down each branch as far as possible, always adding to the level count.
- When you reach the end of a branch (a leaf), remember the total level count for that branch.
- Go back up and repeat the process for every other possible branch from the root.
- Once you've checked every single possible path from the root to the end of the tree, compare all the level counts you remembered.
- The largest level count you found is the maximum depth of the tree.
Code Implementation
def max_depth_n_ary_tree_brute_force(root):
if not root:
return 0
maximum_depth = 0
def calculate_depth(node, current_depth):
nonlocal maximum_depth
# If the node is a leaf, update the maximum depth if needed.
if not node.children:
maximum_depth = max(maximum_depth, current_depth)
return
# Iterate through children and recursively calculate depth
for child_node in node.children:
calculate_depth(child_node, current_depth + 1)
#Initiate depth calculation from the root.
calculate_depth(root, 1)
return maximum_depthBig(O) Analysis
Optimal Solution
Approach
The best way to find the maximum depth of a tree is to explore it systematically, layer by layer. We visit each part of the tree, figuring out the depth of each branch and picking the deepest one we find.
Here's how the algorithm would work step-by-step:
- Start at the very top of the tree (the root).
- Look at all the branches (children) coming out of the root.
- For each branch, imagine going down that branch and figuring out how deep that part of the tree is. This involves doing the same steps for each child node: look at *its* branches and so on.
- Keep track of the deepest branch you find as you explore each child.
- Once you've looked at all the branches coming out of the root, the deepest branch you found plus one (for the root itself) is the maximum depth of the entire tree.
Code Implementation
class Node:
def __init__(self, val=None, children=None):
self.val = val
self.children = children if children is not None else []
def max_depth_n_ary(root: 'Node') -> int:
if not root:
return 0
maximum_children_depth = 0
# Iterate through all the children of the current node.
for child in root.children:
# Recursively find the maximum depth of each child subtree.
child_depth = max_depth_n_ary(child)
maximum_children_depth = max(maximum_children_depth, child_depth)
# Add 1 to account for the current node's depth.
return maximum_children_depth + 1Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or Empty Tree (root is null) | Return 0 immediately as an empty tree has a depth of 0. |
| Single Node Tree (root with no children) | Return 1 as a single node tree has a depth of 1. |
| Tree with very deep single path (highly skewed distribution) | The algorithm should still work correctly, but the recursion depth might become a concern depending on language limitations and stack size. |
| Tree with a very wide branching factor, but shallow depth | Algorithm will handle this efficiently as it explores all branches, limited by the depth, not width. |
| Extremely large tree (memory constraints) | If the tree is too large, a stack overflow could occur with recursion, consider iterative approach to minimize memory footprint. |
| Root node having empty list of children. | The iterative or recursive solution treats this case as a leaf node when iterating through children. |
| Negative or zero values in node data (if node data is used in computation, not depth) | The depth algorithm is independent of the actual values in the nodes, so negative/zero values are irrelevant. |
| Tree where all paths have the same depth | The algorithm will correctly compute and return this depth regardless of whether paths are different. |