Number of Closed Islands
MediumGiven a 2D grid consists of 0s (land) and 1s (water). An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.
Return the number of closed islands.
Example 1:
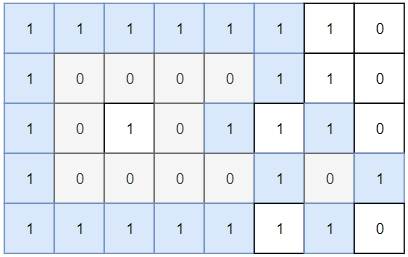
Input: grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]] Output: 2 Explanation: Islands in gray are closed because they are completely surrounded by water (group of 1s).
Example 2:

Input: grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]] Output: 1
Example 3:
Input: grid = [[1,1,1,1,1,1,1],
[1,0,0,0,0,0,1],
[1,0,1,1,1,0,1],
[1,0,1,0,1,0,1],
[1,0,1,1,1,0,1],
[1,0,0,0,0,0,1],
[1,1,1,1,1,1,1]]
Output: 2
Constraints:
1 <= grid.length, grid[0].length <= 1000 <= grid[i][j] <=1
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions of the grid (rows and columns)? What is the maximum size I should expect?
- Can the grid be empty (zero rows or zero columns)? What should I return in that case?
- Is the input grid guaranteed to only contain 0s and 1s, or could there be other values?
- How do you define 'four-directionally connected'? Should I only consider up, down, left, and right?
- If an island touches the boundary in only one place, is it still considered not closed?
Brute Force Solution
Approach
We are given a map of land and water and we want to find the islands completely surrounded by water. The brute force way is to check every single piece of land to see if it's part of a closed island.
Here's how the algorithm would work step-by-step:
- Go through each piece of land on the map, one by one.
- For each piece of land, explore all the connected land around it.
- While exploring, check if you ever reach the edge of the map.
- If you reach the edge of the map, then the island isn't closed, so stop exploring it and move on to the next piece of land.
- If you explore all the connected land and never reach the edge of the map, then you've found a closed island, so count it.
- Keep doing this until you've checked every single piece of land on the map.
Code Implementation
def number_of_closed_islands(grid): rows = len(grid)
cols = len(grid[0])
number_of_closed_islands_found = 0
def explore_island(row, col, visited):
if (row < 0 or row >= rows or col < 0 or col >= cols):
return False
if grid[row][col] == 1 or (row, col) in visited:
return True
visited.add((row, col))
# Recursively explore adjacent land cells
up = explore_island(row - 1, col, visited)
down = explore_island(row + 1, col, visited)
left = explore_island(row, col - 1, visited)
right = explore_island(row, col + 1, visited)
return up and down and left and right
for row in range(rows):
for col in range(cols):
if grid[row][col] == 0:
# Start exploring if it's a land cell
is_closed = explore_island(row, col, set())
# Increment count if fully closed
if is_closed:
number_of_closed_islands_found += 1
return number_of_closed_islands_foundBig(O) Analysis
Optimal Solution
Approach
The challenge is to find enclosed 'land' areas in a grid surrounded by 'water'. The smart way to solve this is to think about what *isn't* an island: anything touching the edges of the grid cannot be a closed island. We eliminate these to make the search easier.
Here's how the algorithm would work step-by-step:
- Start by looking at the edges of the grid. Any piece of 'land' connected to an edge cannot be part of a closed island.
- Treat any 'land' touching an edge as if it were 'water'. This is done by changing the land to water.
- Keep spreading this 'water' effect to any adjacent 'land'. Basically, flood everything connected to the boundary.
- Now, look at the remaining 'land' within the grid. Any 'land' left must be entirely surrounded by 'water' – a closed island.
- Count the number of these remaining 'land' areas. Each separate 'land' area is a closed island.
Code Implementation
def number_of_closed_islands(grid):
rows = len(grid)
cols = len(grid[0])
def depth_first_search(row, col):
if row < 0 or row >= rows or col < 0 or col >= cols or grid[row][col] == 1:
return
grid[row][col] = 1
depth_first_search(row + 1, col)
depth_first_search(row - 1, col)
depth_first_search(row, col + 1)
depth_first_search(row, col - 1)
# Eliminate islands connected to the boundary
for row in range(rows):
for col in range(cols):
if row == 0 or row == rows - 1 or col == 0 or col == cols - 1:
if grid[row][col] == 0:
# Flood fill from boundary land
depth_first_search(row, col)
closed_islands_count = 0
# Count remaining closed islands
for row in range(rows):
for col in range(cols):
if grid[row][col] == 0:
# Count the islands not connected to an edge
closed_islands_count += 1
# Flood fill so we don't double count
depth_first_search(row, col)
return closed_islands_countBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or Empty Grid | Return 0 immediately as there are no islands to evaluate. |
| Grid with all 1s (water) | Return 0, since no land exists to form an island. |
| Grid with all 0s (land) | Return 0 if any 0 touches the boundary; otherwise, return 1 if the entire grid is enclosed by water outside the given grid. |
| 1x1 Grid with a single 0 | Return 0, as it always touches the boundary. |
| 1xN or Nx1 Grid with any 0s | Return 0, since any 0 in such grids will be connected to the boundary. |
| Large grid (N x M where N and M are large) | The solution needs to be efficient with memory, potentially favoring iterative DFS or BFS to manage recursion depth if using a recursive DFS solution. |
| Island touching the boundary at multiple disconnected points | The DFS/BFS should flag the entire island as not closed if any part of it touches the boundary. |
| Integer overflow during grid traversal in extremely large grids | The data structure used for grid size, row, and column indices, should be able to hold all possible values; most languages will do this automatically, but it should be considered during implementation. |