Count Submatrices With All Ones
MediumGiven an m x n binary matrix mat, return the number of submatrices that have all ones.
Example 1:
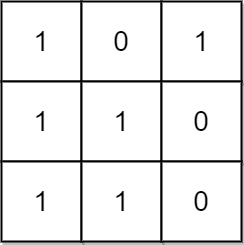
Input: mat = [[1,0,1],[1,1,0],[1,1,0]] Output: 13 Explanation: There are 6 rectangles of side 1x1. There are 2 rectangles of side 1x2. There are 3 rectangles of side 2x1. There is 1 rectangle of side 2x2. There is 1 rectangle of side 3x1. Total number of rectangles = 6 + 2 + 3 + 1 + 1 = 13.
Example 2:

Input: mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]] Output: 24 Explanation: There are 8 rectangles of side 1x1. There are 5 rectangles of side 1x2. There are 2 rectangles of side 1x3. There are 4 rectangles of side 2x1. There are 2 rectangles of side 2x2. There are 2 rectangles of side 3x1. There is 1 rectangle of side 3x2. Total number of rectangles = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24.
Constraints:
1 <= m, n <= 150mat[i][j]is either0or1.
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What are the dimensions (rows and columns) constraints for the input matrix?
- Can the matrix be empty (0 rows or 0 columns), or contain null/undefined values?
- Is the matrix guaranteed to only contain 0s and 1s, or could there be other integer values?
- If no submatrices with all ones exist, what should the function return (e.g., 0, -1, null)?
- Are we counting overlapping submatrices as distinct (e.g., a single 1x1 cell inside a larger submatrix)?
Brute Force Solution
Approach
The brute force approach is all about trying every possible submatrix and seeing if it meets our condition (all ones). We examine each possible top-left and bottom-right corner combination and check if the formed submatrix contains only ones.
Here's how the algorithm would work step-by-step:
- Consider every possible top-left corner of a submatrix within the given matrix.
- For each top-left corner, consider every possible bottom-right corner of a submatrix that starts at that top-left corner.
- Given a top-left and bottom-right corner, check every single cell within the submatrix that these corners define to make sure they are all ones.
- If all cells in the submatrix are ones, then increment the count of valid submatrices.
- Repeat the process by trying all combinations of top-left and bottom-right corners.
- Finally, return the total count of valid submatrices which will give us our final answer.
Code Implementation
def count_submatrices_with_ones_brute_force(matrix):
number_of_rows = len(matrix)
number_of_columns = len(matrix[0]) if number_of_rows > 0 else 0
count_of_valid_submatrices = 0
for top_row in range(number_of_rows):
for left_column in range(number_of_columns):
# Iterate through all possible bottom-right corners.
for bottom_row in range(top_row, number_of_rows):
for right_column in range(left_column, number_of_columns):
is_valid_submatrix = True
# Check each cell in the submatrix.
for row in range(top_row, bottom_row + 1):
for column in range(left_column, right_column + 1):
if matrix[row][column] == 0:
is_valid_submatrix = False
break
if not is_valid_submatrix:
break
# Increment counter if submatrix is valid.
if is_valid_submatrix:
count_of_valid_submatrices += 1
return count_of_valid_submatrices
def count_submatrices_with_ones(matrix):
number_of_rows = len(matrix)
number_of_columns = len(matrix[0]) if number_of_rows > 0 else 0
count_of_valid_submatrices = 0
for top_row in range(number_of_rows):
for left_column in range(number_of_columns):
# Iterate through all possible bottom-right corners.
for bottom_row in range(top_row, number_of_rows):
for right_column in range(left_column, number_of_columns):
is_valid_submatrix = True
# Check each cell in the submatrix.
for row in range(top_row, bottom_row + 1):
for column in range(left_column, right_column + 1):
if matrix[row][column] == 0:
is_valid_submatrix = False
break
if not is_valid_submatrix:
break
# Increment counter if submatrix is valid.
if is_valid_submatrix:
count_of_valid_submatrices += 1
return count_of_valid_submatricesBig(O) Analysis
Optimal Solution
Approach
We want to count submatrices filled with ones as quickly as possible. The clever approach focuses on calculating, for each cell, the height of consecutive ones extending upwards, then uses this information to efficiently calculate the number of submatrices ending at that cell.
Here's how the algorithm would work step-by-step:
- For each position in the grid, calculate how many consecutive ones appear vertically above it, including the cell itself.
- Now, go through the grid again. For each position, use the previously calculated heights to determine the maximum width a submatrix of ones can have, ending at that position and using that position's row.
- When determining the maximum width, consider the shortest height observed so far in the row to the left.
- The maximum width at each position represents the number of submatrices that end at that position.
- Add up the number of submatrices found at each position to get the total count.
Code Implementation
def count_submatrices_with_all_ones(matrix):
number_of_rows = len(matrix)
number_of_columns = len(matrix[0]) if number_of_rows > 0 else 0
heights = [[0] * number_of_columns for _ in range(number_of_rows)]
# Calculate heights of consecutive ones
for column_index in range(number_of_columns):
for row_index in range(number_of_rows):
if matrix[row_index][column_index] == 1:
heights[row_index][column_index] = (heights[row_index - 1][column_index] + 1
if row_index > 0 else 1)
total_submatrices = 0
# Iterate and calculate submatrices ending at each cell
for row_index in range(number_of_rows):
for column_index in range(number_of_columns):
if matrix[row_index][column_index] == 1:
min_height = float('inf')
width = 0
# Calculate width based on minimum height to the left
for k in range(column_index, -1, -1):
min_height = min(min_height, heights[row_index][k])
# Width is limited by the shortest height
if min_height > 0:
width += 1
else:
break
# Number of submatrices ending at this cell
total_submatrices += width
return total_submatricesBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty matrix | Return 0 if the input matrix is null or has zero rows/columns. |
| Matrix with a single row or column | The algorithm should still correctly count submatrices in these cases, iterating through the single row or column. |
| Matrix with all zeros | The solution should return 0 since no submatrix can contain all ones. |
| Matrix with all ones | The solution must efficiently count all possible submatrices that can be formed with all ones; this requires efficient computation of submatrix count. |
| Large matrix dimensions that could lead to integer overflow during counting. | Use a 64-bit integer type to store the count of submatrices to prevent overflow. |
| Matrix with alternating rows of ones and zeros | The solution must correctly handle the varying widths of valid submatrices and their counts, not overcounting or undercounting. |
| Matrix with a single '1' surrounded by zeros. | The solution correctly identifies and counts this single-cell submatrix. |
| Rectangular matrix (different number of rows and columns) | Ensure the algorithm correctly handles rectangular matrices without assuming a square shape in any iteration. |