Cousins in Binary Tree II
MediumGiven the root of a binary tree, replace the value of each node in the tree with the sum of all its cousins' values.
Two nodes of a binary tree are cousins if they have the same depth with different parents.
Return the root of the modified tree.
Note that the depth of a node is the number of edges in the path from the root node to it.
Example 1:
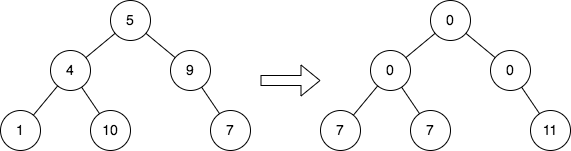
Input: root = [5,4,9,1,10,null,7] Output: [0,0,0,7,7,null,11] Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node. - Node with value 5 does not have any cousins so its sum is 0. - Node with value 4 does not have any cousins so its sum is 0. - Node with value 9 does not have any cousins so its sum is 0. - Node with value 1 has a cousin with value 7 so its sum is 7. - Node with value 10 has a cousin with value 7 so its sum is 7. - Node with value 7 has cousins with values 1 and 10 so its sum is 11.
Example 2:

Input: root = [3,1,2] Output: [0,0,0] Explanation: The diagram above shows the initial binary tree and the binary tree after changing the value of each node. - Node with value 3 does not have any cousins so its sum is 0. - Node with value 1 does not have any cousins so its sum is 0. - Node with value 2 does not have any cousins so its sum is 0.
Constraints:
- The number of nodes in the tree is in the range
[1, 105]. 1 <= Node.val <= 104
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the range of values that the nodes in the binary tree can hold? Can they be negative or zero?
- What should I return if the input tree is null or empty?
- Can the binary tree be unbalanced, skewed, or degenerate (a tree where each node has only one child)?
- Is there any limit to the depth of the binary tree?
- By 'cousins', do you strictly mean nodes at the same level that have different parents, or are we considering nodes that are siblings to be cousins as well (different parents not required)?
Brute Force Solution
Approach
To find the 'cousins' in a family tree where we need to adjust each family member's value based on their 'aunts and uncles', the brute force approach involves looking at each member individually. We will calculate the new value for each member by exhaustively checking the values of everyone else at their level.
Here's how the algorithm would work step-by-step:
- For each person in the family tree, identify their level (how far down they are from the top).
- Find all the other people who are on the same level as that person.
- Sum up the values of all those other people who share the same level as the person's parent, excluding the person's parents themselves. In other words, find the values of all the 'aunts and uncles'.
- Give the person this calculated sum as their new value.
- Repeat this process for every single person in the family tree, level by level.
Code Implementation
class TreeNode:
def __init__(self, value=0, left=None, right=None):
self.value = value
self.left = left
self.right = right
def cousins_in_binary_tree_ii_brute_force(root):
if not root:
return None
# Function to get the level of a node
def get_level(node, target_node, level):
if not node:
return -1
if node == target_node:
return level
left_level = get_level(node.left, target_node, level + 1)
if left_level != -1:
return left_level
return get_level(node.right, target_node, level + 1)
# Function to get all nodes at a specific level
def get_nodes_at_level(node, level, current_level, nodes):
if not node:
return
if current_level == level:
nodes.append(node)
return
get_nodes_at_level(node.left, level, current_level + 1, nodes)
get_nodes_at_level(node.right, level, current_level + 1, nodes)
# Traverse the tree and update node values
nodes_to_process = []
def traverse(node):
if not node:
return
nodes_to_process.append(node)
traverse(node.left)
traverse(node.right)
traverse(root)
for current_node in nodes_to_process:
node_level = get_level(root, current_node, 0)
all_nodes_at_level = []
get_nodes_at_level(root, node_level, 0, all_nodes_at_level)
# Need to determine the parent of the current node
def find_parent(node, target_node, parent):
if not node:
return None
if node.left == target_node or node.right == target_node:
return node
parent_node = find_parent(node.left, target_node, node)
if parent_node:
return parent_node
return find_parent(node.right, target_node, node)
parent_node = find_parent(root, current_node, None)
aunts_uncles_sum = 0
# If the current node has a parent
if parent_node:
parent_level = get_level(root, parent_node, 0)
all_nodes_at_parent_level = []
get_nodes_at_level(root, parent_level, 0, all_nodes_at_parent_level)
# Calculate the sum of aunts and uncles values
for potential_uncle_aunt in all_nodes_at_parent_level:
if potential_uncle_aunt != parent_node:
aunts_uncles_sum += potential_uncle_aunt.value
# Update the current node's value with the sum of aunts and uncles
current_node.value = aunts_uncles_sum
return rootBig(O) Analysis
Optimal Solution
Approach
The problem asks us to modify values in a binary tree. The efficient solution focuses on processing the tree level by level, computing the sum of nodes at each level, and then using that sum to update the node values. This avoids redundant calculations by only traversing the tree once per level.
Here's how the algorithm would work step-by-step:
- Begin by processing the root of the tree. The root's value will be updated to zero, since it has no siblings.
- Then, proceed level by level down the tree.
- At each level, first compute the sum of all the node values on that level. This represents the total value of all nodes that could be cousins of each other.
- Now, traverse the nodes again at that same level. For each node, subtract its own value from the total level sum.
- Update the node's value to be the remaining sum (the level sum without its own value). This remaining sum represents the combined value of its siblings (or cousins at that level).
- Continue this process level by level until all nodes in the tree have been processed. This approach ensures each node's new value is correct and calculated efficiently.
Code Implementation
from collections import deque
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def replaceValueInTree(root):
if not root:
return root
root.val = 0
queue = deque([root])
while queue:
level_length = len(queue)
level_nodes = []
for _ in range(level_length):
node = queue.popleft()
level_nodes.append(node)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
# Calculate the sum of the current level.
level_sum = sum(node.val for node in level_nodes)
# Update the values of the nodes in the current level.
for node in level_nodes:
subtree_sum = 0
if node.left:
subtree_sum += node.left.val
if node.right:
subtree_sum += node.right.val
# This prevents modifying the original sum
node_value = node.val
node.val = level_sum - node_value
return rootBig(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null root node | Return null immediately as there is no tree to process. |
| Tree with only the root node | The root's value becomes 0 as it has no siblings. |
| Tree with two nodes, root and one child | The child's value becomes 0 as it has no siblings. |
| Complete binary tree with a large number of nodes, potential for integer overflow when summing level values | Use a larger data type like long to store the level sum and avoid potential overflow. |
| Skewed tree (e.g., only left children) | The level-order traversal correctly handles skewed trees, calculating siblings' sums level by level. |
| Deeply nested tree, potential for stack overflow if recursion is used without optimization | Use iterative level-order traversal instead of recursion to avoid stack overflow errors. |
| Tree with nodes having large integer values | Ensure data types used to store node values and level sums can accommodate the potentially large values. |
| Nodes with negative integer values | The algorithm works correctly with negative values, as the sum can be negative as well. |