Frog Position After T Seconds
HardGiven an undirected tree consisting of n vertices numbered from 1 to n. A frog starts jumping from vertex 1. In one second, the frog jumps from its current vertex to another unvisited vertex if they are directly connected. The frog can not jump back to a visited vertex. In case the frog can jump to several vertices, it jumps randomly to one of them with the same probability. Otherwise, when the frog can not jump to any unvisited vertex, it jumps forever on the same vertex.
The edges of the undirected tree are given in the array edges, where edges[i] = [ai, bi] means that exists an edge connecting the vertices ai and bi.
Return the probability that after t seconds the frog is on the vertex target. Answers within 10-5 of the actual answer will be accepted.
Example 1:
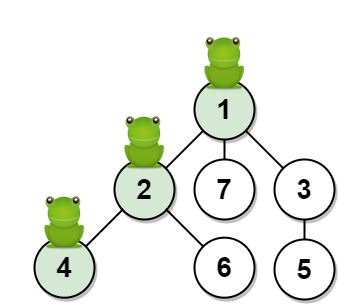
Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4 Output: 0.16666666666666666 Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 probability to the vertex 2 after second 1 and then jumping with 1/2 probability to vertex 4 after second 2. Thus the probability for the frog is on the vertex 4 after 2 seconds is 1/3 * 1/2 = 1/6 = 0.16666666666666666.
Example 2:

Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7 Output: 0.3333333333333333 Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 = 0.3333333333333333 probability to the vertex 7 after second 1.
Constraints:
1 <= n <= 100edges.length == n - 1edges[i].length == 21 <= ai, bi <= n1 <= t <= 501 <= target <= n
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- Is the graph represented by 'edges' always a tree (connected and acyclic), or could there be cycles or disconnected components?
- What should I return if the frog cannot reach the target node within T seconds? Is a probability of 0 acceptable?
- Can the values in 'edges' contain node indices that are out of range (e.g., larger than n)? Should I assume nodes are 1-indexed or 0-indexed?
- If the frog reaches the target node before T seconds and there are no unvisited neighboring nodes, should the frog stay at the target, or does it disappear and have probability 0?
- What are the constraints on the values of n and T? Could n or T be very large?
Brute Force Solution
Approach
The frog starts at position 1. We want to find the probability the frog is at the target position after a certain time. The brute force method explores every possible path the frog can take during that time, checking if the frog ends up at the target.
Here's how the algorithm would work step-by-step:
- Start with the frog at position 1.
- Consider all the possible places the frog can jump to in the first second.
- For each of those places, consider all the places the frog can jump to in the second second.
- Keep doing this until you've considered all the jumps for the given amount of time.
- For each possible path, check if the frog ends up at the target position after all the jumps.
- If the frog ends up at the target position, calculate the probability of taking that particular path.
- Add up the probabilities of all the paths that lead to the target position.
- The total probability is the answer.
Code Implementation
def frog_position_brute_force(number_of_nodes, edges, time, target): graph = [[] for _ in range(number_of_nodes + 1)]
for start_node, end_node in edges:
graph[start_node].append(end_node)
graph[end_node].append(start_node)
def get_probability(current_node, current_time, visited):
if current_time == time:
if current_node == target:
return 1.0
else:
return 0.0
neighbors = [neighbor for neighbor in graph[current_node] if neighbor not in visited]
#Handle the case when stuck at a leaf node
if not neighbors:
if current_node == target:
return 1.0
else:
return 0.0
probability = 0.0
number_of_neighbors = len(neighbors)
# Iterate through each neighbor and calculate its probability
for neighbor in neighbors:
new_visited = set(visited)
new_visited.add(neighbor)
probability += get_probability(neighbor, current_time + 1, new_visited) / number_of_neighbors
return probability
visited_nodes = {1}
#Start the search from Node 1
return get_probability(1, 0, visited_nodes)Big(O) Analysis
Optimal Solution
Approach
We need to simulate the frog's jumps through the tree, figuring out where it ends up after a certain amount of time. The key is to use a method that efficiently explores the tree while considering probabilities at each jump, stopping early if we reach our target or run out of time.
Here's how the algorithm would work step-by-step:
- Begin at the starting node (node 1).
- Simulate the frog's movement one second at a time, up to the specified time limit.
- At each node, determine the possible next hops, but only to unvisited (new) nodes.
- If the frog has multiple options for the next hop, divide the probability of being at the current node evenly among those options.
- If the frog reaches the target node at any point, store the probability of being there. Do not continue jumping after reaching the target unless more time remains and it has unvisited children.
- If the frog has no unvisited nodes to jump to or the time runs out, stop simulating.
- If the frog ends at the target node, return the accumulated probability of being there; otherwise, return zero.
Code Implementation
def frog_position(number_of_nodes, edges, time, target): graph = [[] for _ in range(number_of_nodes + 1)]
for start_node, end_node in edges:
graph[start_node].append(end_node)
graph[end_node].append(start_node)
probabilities = [0.0] * (number_of_nodes + 1)
probabilities[1] = 1.0
visited = [False] * (number_of_nodes + 1)
visited[1] = True
current_node = 1
for _ in range(time):
next_probabilities = [0.0] * (number_of_nodes + 1)
for current_node in range(1, number_of_nodes + 1):
if probabilities[current_node] > 0:
unvisited_neighbors = []
for neighbor in graph[current_node]:
if not visited[neighbor]:
unvisited_neighbors.append(neighbor)
number_of_possible_jumps = len(unvisited_neighbors)
# If no unvisited neighbors, stay put
if number_of_possible_jumps == 0:
next_probabilities[current_node] += probabilities[current_node]
else:
probability_per_jump = probabilities[current_node] / number_of_possible_jumps
for next_node in unvisited_neighbors:
next_probabilities[next_node] = probability_per_jump
probabilities = next_probabilities
for node_index in range(1, number_of_nodes + 1):
if probabilities[node_index] > 0 and not visited[node_index]:
visited[node_index] = True
# Return probability of frog being at target
return probabilities[target]Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| n = 1, T > 0, target != 1 | The frog starts at node 1 and can't reach any other node, so return False since it cannot reach the target |
| T = 0, target != 1 | The frog starts at node 1; if the target isn't 1, return False as the frog can't move in 0 seconds |
| Tree is disconnected (unreachable target) | Return false if the target is unreachable from the starting node (node 1) after T seconds. |
| Target node is a leaf node and T is large enough to reach it | Check if the frog stays at the target node after reaching it if it's a leaf and time remains |
| Target node is an internal node, and T is large enough to reach it | If time remains after arriving at the target non-leaf node, the frog must have no unvisited neighbors to remain at that node |
| Large number of nodes and edges, deep tree | Ensure the solution (e.g., BFS/DFS) doesn't exceed recursion depth limits or memory constraints. |
| Graph has cycles (but is described as a tree) | Maintain a 'visited' set to prevent infinite loops when exploring the graph, effectively treating it as a tree during traversal. |
| Integer overflow when calculating time | Use appropriate data types (e.g., long) to avoid potential integer overflows when handling large values of T or node counts. |