Valid Mountain Array
EasyGiven an array of integers arr, return true if and only if it is a valid mountain array.
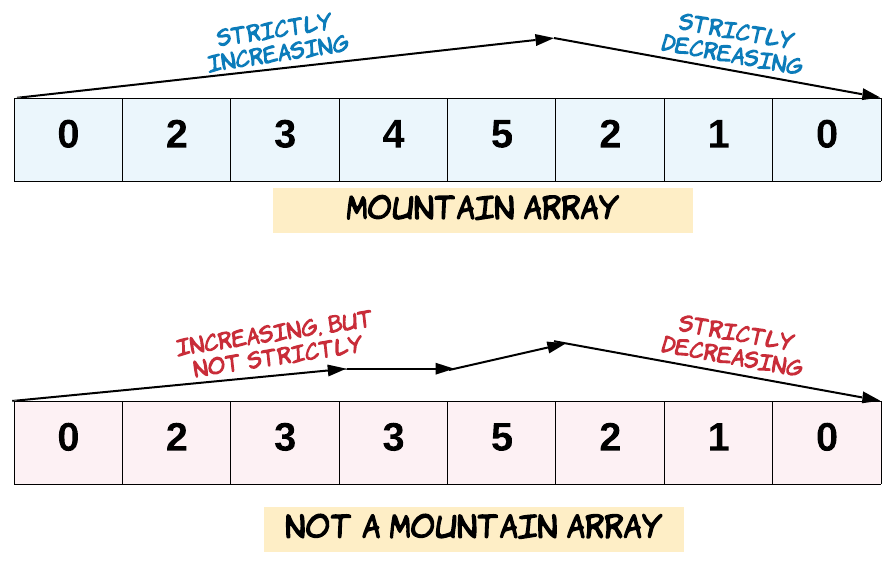
Recall that arr is a mountain array if and only if:
arr.length >= 3- There exists some
iwith0 < i < arr.length - 1such that:arr[0] < arr[1] < ... < arr[i - 1] < arr[i]arr[i] > arr[i + 1] > ... > arr[arr.length - 1]
Example 1:
Input: arr = [2,1] Output: false
Example 2:
Input: arr = [3,5,5] Output: false
Example 3:
Input: arr = [0,3,2,1] Output: true
Constraints:
1 <= arr.length <= 1040 <= arr[i] <= 104
Solution
Clarifying Questions
When you get asked this question in a real-life environment, it will often be ambiguous (especially at FAANG). Make sure to ask these questions in that case:
- What is the minimum length of the array? Is an array with length less than 3 considered a mountain array?
- Can the input array contain non-integer values (e.g., floats)?
- Can the values in the array be negative or zero?
- If there are multiple peaks in the array, is it still considered a valid mountain array?
- What should I return if the input array is null or empty?
Brute Force Solution
Approach
The brute force approach to identifying a mountain involves checking every possible place where the peak could be. We verify that the numbers increase until the potential peak, then decrease after the peak.
Here's how the algorithm would work step-by-step:
- Assume that the first number is the peak and verify the criteria for a mountain.
- If this doesn't match then assume the second number is the peak and again verify the criteria for a mountain.
- Repeat this process for every number as a potential peak.
- A valid mountain array will only be identified when one of the numbers as a peak satisfies the increasing before peak and decreasing after peak condition.
Code Implementation
def valid_mountain_array_brute_force(numbers):
array_length = len(numbers)
for potential_peak_index in range(array_length):
# Peak cannot be the first or last element
if potential_peak_index == 0 or potential_peak_index == array_length - 1:
continue
is_valid_mountain = True
# Check increasing sequence before the peak
for index_before_peak in range(potential_peak_index):
if numbers[index_before_peak] >= numbers[index_before_peak + 1]:
is_valid_mountain = False
break
# Check decreasing sequence after the peak
if is_valid_mountain:
for index_after_peak in range(potential_peak_index, array_length - 1):
if numbers[index_after_peak] <= numbers[index_after_peak + 1]:
is_valid_mountain = False
break
# We have found a valid peak
if is_valid_mountain:
return True
# If no valid peak is found, return False
return FalseBig(O) Analysis
Optimal Solution
Approach
We want to check if a group of numbers looks like a mountain: first going up, then coming down. The key idea is to walk through the numbers and confirm that we first move upward to the peak, and then downward after reaching the peak. We can avoid unnecessary checks by stopping early if the 'mountain' shape is broken at any point.
Here's how the algorithm would work step-by-step:
- Start at the beginning of the numbers.
- Keep moving forward as long as each number is bigger than the one before it. This shows we are climbing the mountain.
- If we reach the end while still climbing, or if we never even started climbing, it's not a mountain.
- Remember the highest point we reached, which is the peak of the mountain.
- Now, keep moving forward as long as each number is smaller than the one before it. This shows we are descending the mountain.
- If we reach the end while still descending, and if we did both climb and descend at some point, then it is a valid mountain.
Code Implementation
def is_valid_mountain_array(arr):
array_length = len(arr)
current_index = 0
# Need at least three elements
if array_length < 3:
return False
# Walk up the mountain
while current_index + 1 < array_length and arr[current_index] < arr[current_index + 1]:
current_index += 1
# Peak can't be the first or last element
if current_index == 0 or current_index == array_length - 1:
return False
# Walk down the mountain
# Make sure we are actually descending now.
while current_index + 1 < array_length and arr[current_index] > arr[current_index + 1]:
current_index += 1
# Check if we reached the end
# It is a valid mountain if we reached the end.
return current_index == array_length - 1Big(O) Analysis
Edge Cases
| Case | How to Handle |
|---|---|
| Null or empty input array | Return false immediately, as a mountain array must have at least 3 elements. |
| Array with only one or two elements | Return false immediately, as a mountain array must have at least 3 elements and both an increasing and decreasing section. |
| Array is strictly increasing or strictly decreasing | Return false, as a mountain array must have both increasing and decreasing portions. |
| Peak is the first or last element | Return false, as the peak cannot be the first or last element in a mountain array, since it needs increasing and decreasing portions before and after the peak, respectively. |
| Array contains duplicate values such that there is no clear peak | The algorithm should still identify whether there is an increasing followed by a decreasing sequence, and return false if it is not consistently trending as mountain range. |
| Array with large number of elements impacting performance | The linear time complexity O(n) of the one-pass or two-pass approach ensures it scales reasonably with large input sizes; no performance issues expected. |
| Integer overflow if calculating differences between elements for very large integer values | This algorithm does not perform arithmetic calculation which can lead to integer overflow issues between elements, as such, no overflow concerns exist here. |
| Array contains negative numbers or zeros | Negative numbers and zeros do not invalidate the mountain array property, so the algorithm handles them correctly as long as the increasing and decreasing sequences are valid. |